
【题目】我国宋朝数学家杨辉在他的著作《详解九章算法》中提出“杨辉三角”(如图),此图揭示了(a+b)n(n为非负整数)展开式的项数及各项系数的有关规律.例如:(a+b)0=1,它只有一项,系数为1;(a+b)1=a+b,它有两项,系数分别为1,1,系数和为2;(a+b)2=a2+2ab+b2,它有三项,系数分别为1,2,1,系数和为4;(a+b)3=a3+3a2b+3ab2+b3,它有四项,系数分别为1,3,3,1,系数和为8……

根据以上规律,解答下列问题:
(1)(a+b)4的展开式共有多少项,系数分别为多少;
(2)写出(a+b)5的展开式;
(3)(a+b)n的展开式共有多少项,系数和为多少.
【答案】(1)5; 1,4,6,4,1;(2)a5+5a4b+10a3b2+10a2b3+5ab4+b5;(3)(n+1); 2n.
【解析】
(1)本题通过阅读理解寻找规律,观察可得(a+b)n(n为非负整数)展开式的各项系数的规律:首尾两项系数都是1,中间各项系数等于(a+b)n-1相邻两项的系数和.因此可得(a+b)4的各项系数分别为1、(1+3)、(3+3)、(3+1)、1即可;
(2)由(1)得出的规律,即可得出结果;
(3)根据题意得出(a+b)n展开式共有(n+1)项,当a=b=1时,(a+b)n=2n即可.
解:(1)根据题意知,(a+b)4的展开后,共有5项,
各项系数分别为1、(1+3)、(3+3)、(3+1)、1,
即:1、4、6、4、1;
(2)根据题意得:(a+b)5的展开式为a5+5a4b+10a3b2+10a2b3+5ab4+b5.
(3)根据题意得:(a+b)n的展开式共有(n+1)项
当a=b=1时,(a+b)n=2n.
即:(a+b)n的展开式系数和为2n.


 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案科目:初中数学 来源: 题型:
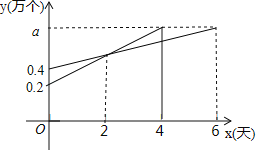
【题目】为了推动校园足球发展,某市教体局准备向全市中小学免费赠送一批足球,这批足球的生产任务由甲、乙两家足球制造企业平均承担,甲企业库存0.2万个,乙企业库存0.4万个,两企业同时开始生产,且每天生产速度不变,甲、乙两家企业生产的足球数量y万个与生产时间x天之间的函数关系如图所示,则每家企业供应的足球数量a等于 万个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在矩形ABCD中,AB=6cm,BC=8cm,对角线AC,BD交于点O,点P从点A出发,沿AD方向匀速运动,速度为1cm/s;同时,点Q从点D出发,沿DC方向匀速运动,速度为1cm/s;当一个点停止运动时,另一个点也停止运动.连接PO并延长,交BC于点E,过点Q作QF∥AC,交BD于点F.设运动时间为t(s)(0<t<6),解答下列问题: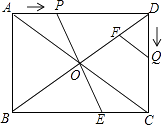
(1)当t为何值时,AP=PO.
(2)设五边形OECQF的面积为S(cm2),试确定S与t的函数关系式;
(3)在运动过程中,是否存在某一时刻t,使OD平分∠COP?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
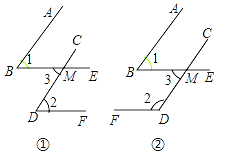
【题目】已知一个角的两边与另一个角的两边分别平行,请结合图,探索这两个角之间的关系,并说明理由.
(1)如图①,AB∥CD,BE∥DF,∠1与∠2的关系是 ;
证明:
(2)如图②,AB∥CD,BE∥DF,∠1与∠2的关系是 ;
证明:
(3)经过上述证明,我们可得出结论,如果一个角的两边与另一个角的两边分别平行,那么这两个角 ;
(4)若这两个角的两边分别平行,且一个角比另一个角的3倍少60°,则这两个角分别是多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为1的小正方形网格中,△AOB的顶点均在格点上.
(1)B点关于y轴的对称点坐标为 ;
(2)将△AOB向左平移3个单位长度得到△A1O1B1,请画出△A1O1B1;
(3)在(2)的条件下,A1的坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣ ![]() x2+bx+c与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
x2+bx+c与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).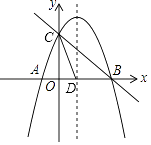
(1)求抛物线的解析式
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,请直接写出P点的坐标;如果不存在,请说明理由.
(3)点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,△CBF的面积最大?请求出△CBF的最大面积及此时E点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
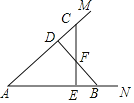
【题目】如图,C,D和E,B分别是∠MAN的边AM和AN上的两点,且AC=AB,AD=AE,CE和BD相交于F点,给出下列结论:①△ABD≌△ACE;②△BFE≌△CFD;③F在∠MAN的平分线上.其中正确的是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com