
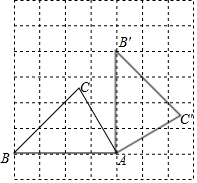
 如图,△ABC的顶点A,B都在格点上,将△ABC绕点A顺时针旋转得到相应的△AB′C′,且点B的对应点B′也在格点上,则∠CAC′的度数为90°.
如图,△ABC的顶点A,B都在格点上,将△ABC绕点A顺时针旋转得到相应的△AB′C′,且点B的对应点B′也在格点上,则∠CAC′的度数为90°.  名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
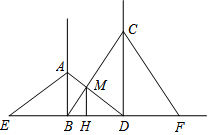 如图,工地上两根电灯杆相距a米,分别在高为4米、6米的A、C处用铁丝将两杆固定,则铁丝AD与铁丝BC的交点M处离地面米的高MH=$\frac{12}{5}$m.
如图,工地上两根电灯杆相距a米,分别在高为4米、6米的A、C处用铁丝将两杆固定,则铁丝AD与铁丝BC的交点M处离地面米的高MH=$\frac{12}{5}$m.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在平面直角坐标系中,边长为1的正方形OA1B1C1的两边在坐标轴上,以它的对角线OB1,为边作正方形OB1B2C2,再以OB1B2C2正方形的对角线OB2为边作正方形OB2B2C3,依此类推…,则正方形OB99B100C100的顶点B100的坐标是( )
如图,在平面直角坐标系中,边长为1的正方形OA1B1C1的两边在坐标轴上,以它的对角线OB1,为边作正方形OB1B2C2,再以OB1B2C2正方形的对角线OB2为边作正方形OB2B2C3,依此类推…,则正方形OB99B100C100的顶点B100的坐标是( )| A. | (2100,0) | B. | (0,250) | C. | (-250,0) | D. | (0,-2100) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
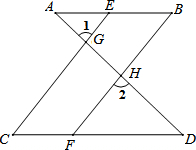 完成下面推理过程:
完成下面推理过程:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com