
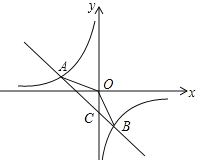
【题目】如图,在平面直角坐标系xOy中,一次函数![]() (a,b为常数,且
(a,b为常数,且![]() )与反比例函数
)与反比例函数![]() (m为常数,且
(m为常数,且![]() )的图象交于点A(﹣2,1)、B(1,n).
)的图象交于点A(﹣2,1)、B(1,n).

(1)求反比例函数和一次函数的解析式;
(2)连结OA、OB,求△AOB的面积;
(3)直接写出当![]() 时,自变量x的取值范围.
时,自变量x的取值范围.
【答案】(1)![]() ,
,![]() ;(2)2;(3)
;(2)2;(3)![]() .
.
【解析】
(1)将A坐标代入反比例函数解析式中求出m的值,即可确定出反比例函数解析式;将B坐标代入反比例解析式中求出n的值,确定出B坐标,将A与B坐标代入一次函数解析式中求出a与b的值,即可确定出一次函数解析式;
(2)设直线AB与y轴交于点C,求得点C坐标,![]() ,计算即可;
,计算即可;
(3)由图象直接可得自变量x的取值范围.
(1)∵A(﹣2,1),
∴将A坐标代入反比例函数解析式![]() 中,得
中,得![]() ,
,
∴反比例函数解析式为![]() ,
,
将B坐标代入![]() ,得
,得![]() ,
,
∴B坐标(1,﹣2),将A与B坐标代入一次函数解析式中,得:![]() ,解得
,解得![]() ,
,
∴一次函数解析式为![]() ;
;
(2)设直线AB与y轴交于点C,令x=0,得y=﹣1,
∴点C坐标(0,﹣1),
∵![]() =
=![]() =2;
=2;
(3)由图象可得,当![]() 时,自变量x的取值范围
时,自变量x的取值范围![]() .
.


科目:初中数学 来源: 题型:
【题目】“五一”前夕,某经销商计划花23500元购买A、B、C三种新款时装共50套进行试销,并且购进的C种时装套数不少于B种时装套数,且不超过A种时装套数,设购进A种时装x套,B种时装y套,三种时装的进价和售价如下表所示.
型号 | A | B | C |
进价(元/套) | 400 | 550 | 500 |
售价(元/套) | 500 | 700 | 650 |
(1)求y与x之间的函数关系式;
(2)满足条件的进货方案有哪几种?写出解答过程;
(3)假设所购进的这三种时装能全部卖出,且在购销这批时装的过程中需要另外支出各种费用1000元.通过计算判断哪种进货方案利润最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
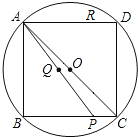
【题目】如图,![]() 内接于⊙O,
内接于⊙O,![]() ,
,![]() 是⊙O上与点
是⊙O上与点![]() 关于圆心
关于圆心![]() 成中心对称的点,
成中心对称的点,![]() 是
是![]() 边上一点,连结
边上一点,连结![]() .已知
.已知![]() ,
,![]() ,
,![]() 是线段
是线段![]() 上一动点,连结
上一动点,连结![]() 并延长交四边形
并延长交四边形![]() 的一边于点
的一边于点![]() ,且满足
,且满足![]() ,则
,则![]() 的值为_______________.
的值为_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣x+5与x轴交于点B,与y轴交于点D,抛物线y=﹣x2+bx+c与直线y=﹣x+5交于B,D两点,点C是抛物线的顶点.

(1)求抛物线的解析式;
(2)点M是直线BD上方抛物线上的一个动点,其横坐标为m,过点M作x轴的垂线,交直线BD于点P,当线段PM的长度最大时,求m的值及PM的最大值;
(3)在抛物线上是否存在异于B、D的点Q,使△BDQ中BD边上的高为3![]() ,若存在求出点Q的坐标;若不存在请说明理由.
,若存在求出点Q的坐标;若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
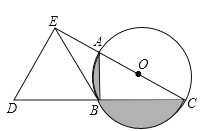
【题目】如图,AC为⊙O的直径,B为⊙O上一点,∠ACB=30°,延长CB至点D,使得CB=BD,过点D作DE⊥AC,垂足E在CA的延长线上,连接BE.
(1)求证:BE是⊙O的切线;
(2)当BE=3时,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮一家在一湖泊中游玩,湖泊中有一孤岛,妈妈在孤岛P处观看小亮与爸爸在湖中划船(如图所示).小船从P处出发,沿北偏东60°方向划行200米到A处,接着向正南方向划行一段时间到B处.在B处小亮观测到妈妈所在的P处在北偏西37°的方向上,这时小亮与妈妈相距多少米(精确到1米)?
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1所示的是某超市入口的双翼闸门,如图2,当它的双翼展开时,双翼边缘的端点A与B 之间的距离为10cm,双翼的边缘AC=BD=54cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°,求当双翼收起时,可以通过闸机的物体的最大宽度。


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 今年5月份,我市某中学开展争做“五好小公民”征文比赛活动,赛后随机抽取了部分参赛学生的成绩,按得分划分为A,B,C,D四个等级,并绘制了如下不完整的频数分布表和扇形统计图:
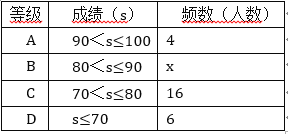
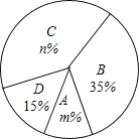
根据以上信息,解答以下问题:
(1)表中的x=______;
(2)扇形统计图中m=______,n=______,C等级对应的扇形的圆心角为______度;
(3)该校准备从上述获得A等级的四名学生中选取两人做为学校“五好小公民”志愿者,已知这四人中有两名男生(用a1,a2表示)和两名女生(用b1,b2表示),请用列表或画树状图的方法求恰好选取的是a1和b1的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
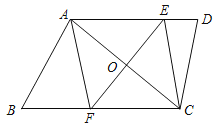
【题目】如图,在四边形ABCD中,AD∥BC,点O是对角线AC的中点,过点O作AC的垂线,分别交AD、BC于点E、F,连结AF、CE.
(1)求证:△AOE≌△COF.
(2)试判断四边形AFCE的形状,并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com