
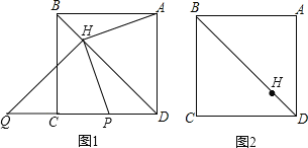
【题目】 已知:在正方形ABCD中,点H在对角线BD上运动(不与B,D重合)连接AH,过H点作HP⊥AH于H交直线CD于点P,作HQ⊥BD于H交直线CD于点Q.
(1)当点H在对角线BD上运动到图1位置时,则CQ与PD的数量关系是______.
(2)当H点运动到图2所示位置时
①依据题意补全图形.
②上述结论还成立吗?若成立,请证明.若不成立,请说明理由.
(3)若正方形边长为![]() ,∠PHD=30°,直接写出PC长.
,∠PHD=30°,直接写出PC长.
【答案】(1)相等;(2)①见解析,②结论成立,见解析;(3)![]() -1或
-1或![]() +1
+1
【解析】
(1)证△ADH≌△PQH得AD=PQ=CD,据此可得CQ=PD;
(2)①根据题意补全图形即可;②连接HC,先证△ADH≌△CDH得∠1=∠2,再证△CQH≌△PDH得出答案;
(3)分以上图1、图2中的两种情况,先求出∠DAP=∠PHD=30°,再由在Rt△ADP中AD=CD=![]() 得出PD=ADtan30°=1,从而得解.
得出PD=ADtan30°=1,从而得解.
解:(1)相等
∵∠AHP=∠DHQ=90°,
∴∠AHD=∠PHQ,
∵四边形ABCD是正方形,
∴∠ADB=∠BDC=∠PQH=45°,AD=CD,
则DH=QH,
∴△ADH≌△PQH(ASA),
∴AD=PQ=CD,
∴CQ=PD,
故答案为:相等.
(2)①依题意补全如图所示,
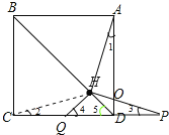
②结论成立,证明如下:
证明:连接HC,
∵正方形ABCD,BD为对角线,
∴∠5=45°,
∵AD=CD、DH=DH,
∴△ADH≌△CDH(SAS),
∴∠1=∠2,
又∵QH⊥BD,∠5=45°,
∴∠4=45°,
∴∠4=∠5,
∴QH=HD,∠HQC=∠HDP=135°,
∵AH⊥HP,AD⊥DP,
∴∠AHP=∠ADP=90°,
又∵∠AOH=∠DOP,
∴∠1=∠3,
∴∠2=∠3,
∴△CQH≌△PDH(AAS)
∴CQ=PD.
(3)如图2,连接AP,

由(1)知△ADH≌△PQH,
∴AH=PH,
∵∠AHP=90°,
∴∠APH=45°,
又∠ADH=45°,∠PHD=30°,
∴∠DAP=∠PHD=30°,
在Rt△ADP中,∵AD=CD=![]() ,
,
∴PD=ADtan30°=1,
则CP=CD-PD=![]() -1;
-1;
如图3,连接AP,
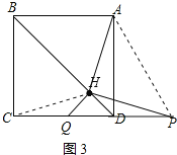
同理可得PD=1,
则CP=![]() +1,
+1,
综上,PC的长度为![]() -1或
-1或![]() +1.
+1.


科目:初中数学 来源: 题型:
【题目】下列实验中,概率最大的是【 】
A. 抛掷一枚质地均匀的硬币,出现正面;
B. 抛掷一枚质地均匀的正方体骰子(六个面分别刻有数字1到6),掷出的点数为奇数;
C. 在一副洗匀的扑克(背面朝上)中任取一张,恰好为方块;
D. 三张同样的纸片,分别写有数字2,3,4,和匀后背面朝上,任取一张恰好为偶数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李在某商场购买![]() 两种商品若干次(每次
两种商品若干次(每次![]() 商品都买) ,其中前两次均按标价购买,第三次购买时,
商品都买) ,其中前两次均按标价购买,第三次购买时,![]() 商品同时打折.三次购买
商品同时打折.三次购买![]() 商品的数量和费用如下表所示:
商品的数量和费用如下表所示:
购买A商品的数量/个 | 购买B商品的数量/个 | 购买总费用/元 | |
第一次 |
|
|
|
第二次 |
|
|
|
第三次 |
|
|
|
(1)求![]() 商品的标价各是多少元?
商品的标价各是多少元?
(2)若小李第三次购买时![]() 商品的折扣相同,则商场是打几折出售这两种商品的?
商品的折扣相同,则商场是打几折出售这两种商品的?
(3)在(2)的条件下,若小李第四次购买商品共花去了
![]() 元,则小李的购买方案可能有哪几种?
元,则小李的购买方案可能有哪几种?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小东设计的“过直线外一点作这条直线的平行线”的尺规作图过程.已知:如图1,直线l及直线l外一点A.
求作:直线AD,使得AD∥l.作法:如图2,
①在直线l上任取一点B,连接AB;
②以点B为圆心,AB长为半径画弧,
交直线l于点C;
③分别以点A,C为圆心,AB长为半径
画弧,两弧交于点D(不与点B重合);
④作直线AD.
所以直线AD就是所求作的直线.根据小东设计的尺规作图过程,完成下面的证明.(说明:括号里填推理的依据)
证明:连接CD.
∵AD=CD=__________=__________,
∴四边形ABCD是 ( ).
∴AD∥l( ).
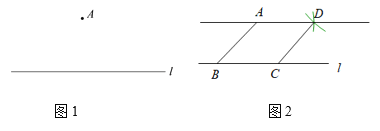
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数y=-x+b的图象与反比例函数y=-![]() 的图象交于点A(-4,a)和B(1,m).
的图象交于点A(-4,a)和B(1,m).
(1)求b的值和点B的坐标;
(2)如果P(n,0)是x轴上一点,过点P作x轴垂线,交一次函数于点M,交反比例函数于点N,当点M在点N上方时,直接写出n的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,
,![]() .点
.点![]() 在
在![]() 上以
上以![]() 的速度由点
的速度由点![]() 向点
向点![]() 运动,同时点
运动,同时点![]() 在
在![]() 上由点
上由点![]() 向点
向点![]() 运动,它们运动的时间为
运动,它们运动的时间为![]() .
.
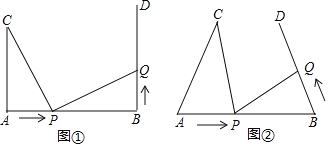
(1)如图①,![]() ,
,![]() ,若点
,若点![]() 的运动速度与点
的运动速度与点![]() 的运动速度相等,当
的运动速度相等,当![]() 时,
时,![]() 与
与![]() 是否全等,请说明理由,并判断此时线段
是否全等,请说明理由,并判断此时线段![]() 和线段
和线段![]() 的位置关系;
的位置关系;
(2)如图②,将图①中的“![]() ,
,![]() ”为改“
”为改“![]() ”,其他条件不变.设点
”,其他条件不变.设点![]() 的运动速度为
的运动速度为![]() ,是否存在实数
,是否存在实数![]() ,使得
,使得![]() 与
与![]() 全等?若存在,求出相应的
全等?若存在,求出相应的![]() 、
、![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖和小红两位同学在学习“概率”时,做投掷骰子(质地均匀的正方体)试验,她们共做了60次试验,试验的结果如下:
朝上的点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现的次数 | 7 | 9 | 6 | 8 | 20 | 10 |
(1)计算“3点朝上”的频率和“5点朝上”的频率.
(2)小颖说:“根据上述试验,一次试验中出现5点朝上的概率最大”;小红说:“如果投掷600次,那么出现6点朝上的次数正好是100次”.小颖和小红的说法正确吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有三个完全相同的小球,分别标有数字3、4、5.从袋子中随机取出一个小球,用小球上的数字作为十位的数字,然后放回;再取出一个小球,用小球上的数字作为个位上的数字,这样组成一个两位数,试问:按这种方法能组成哪些位数?十位上的数字与个位上的数字之和为9的两位数的概率是多少?用列表法或画树状图法加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,测量人员在山脚A处测得山顶B的仰角为45°,沿着仰角为30°的山坡前进1000米到达D处,在D处测得山顶B的仰角为60°,求山的高度?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com