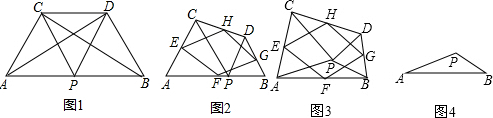
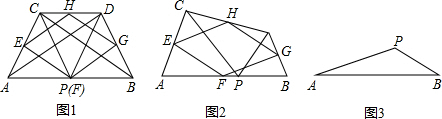
解:(1)四边形EFGH的形状是菱形;
(2)第一问的结论仍成立,即四边形EFGH为菱形,理由为:
连接AD,BC,如图2所示,
∵∠APC=∠BPD,
∴∠APC+∠CPD=∠BPD+∠CPD,即∠APD=∠CPB,
在△APD和△CPB中,
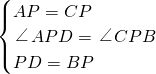
,
∴△APD≌△CPB(SAS),
∴AD=BC,
在△ACD中,E为AC中点,H为CD中点,
∴EH为△ACD的中位线,
∴EH=

AD,EH∥AD,
同理PG=

AD,PG∥AD,HG=

AC,
∴EH=PG,EH∥PG,且EH=HG,
四边形EFGH为菱形;
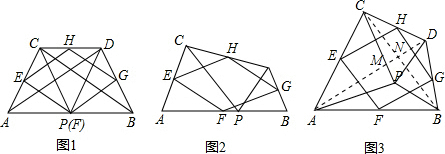
(3)四边形EFGH为正方形,理由为:
连接AD,BC,如图3所示,
∵∠APC=∠BPD,
∴∠APC+∠CPD=∠BPD+∠CPD,即∠APD=∠CPB,
在△APD和△CPB中,
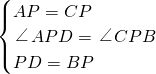
,
∴△APD≌△CPB(SAS),
∴AD=BC,∠DAP=∠BCP,
在△ACD中,E为AC中点,H为CD中点,
∴EH为△ACD的中位线,
∴EH=

AD,EH∥AD,
同理PG=

FG,PG∥AD,HG=

AC,
∴EH=PG,EH∥PG,且EH=HG,
四边形EFGH为菱形,
又∠CMN=∠AMP,∠DAP=∠BCP,
∴△CMN∽△AMP,又∠APC=90°,
∴∠CNM=∠APC=90°,
∴四边形EFGH为正方形.
故答案为:正方形
分析:(1)四边形EFGH为菱形,可以由EH为三角形ACD的中位线,根据中位线定理得到EH平行与AD,且EH等于AD的一半,同理由PG为三角形ABD的中位线,得到PG平行于AD,且PG等于AD的一半,可得出EH与PG平行且相等,得到EFGH为平行四边形,再由三角形APC与三角形BDP都为等边三角形且P为AB的中点,可得出AP=CP,PD=PB,且∠APD=∠CPB=120°,利用SAS得到三角形APD与三角形CPB全等,根据全等三角形的对应边相等可得出AD=BC,再由三角形中位线定理得到HG为BC的一半,等量代换可得出HE=HG,得到平行四边形为菱形;
(2)(1)的结论仍成立,理由为:连接AD,BC,如图2所示,可以由EH为三角形ACD的中位线,根据中位线定理得到EH平行与AD,且EH等于AD的一半,同理由PG为三角形ABD的中位线,得到PG平行于AD,且PG等于AD的一半,可得出EH与PG平行且相等,得到EFGH为平行四边形,由∠APC=∠BPD,两边都加上∠CPD,可得出∠APD=∠CPB,再由AP=CP,DP=BP,利用SAS可得出三角形APD与三角形CPB全等,根据全等三角形的对应边相等可得出AD=BC,再由三角形中位线定理得到HG为BC的一半,等量代换可得出HE=HG,得到平行四边形为菱形;
(3)根据题意补充图形,连接AD,BC,如图3所示,可以由EH为三角形ACD的中位线,根据中位线定理得到EH平行与AD,且EH等于AD的一半,同理由PG为三角形ABD的中位线,得到PG平行于AD,且PG等于AD的一半,可得出EH与PG平行且相等,得到EFGH为平行四边形,由∠APC=∠BPD,两边都加上∠CPD,可得出∠APD=∠CPB,再由AP=CP,DP=BP,利用SAS可得出三角形APD与三角形CPB全等,根据全等三角形的对应边相等可得出AD=BC,再由三角形中位线定理得到HG为BC的一半,等量代换可得出HE=HG,得到平行四边形为菱形.
点评:此题考查了三角形的中位线定理,菱形的判定,全等三角形的判定与性质,以及等边三角形的性质,利用了数形结合及等量代换的思想,本题三问的方法类似,注意2、3小题连接AD与BC,构造全等三角形得到AD=BC,然后利用三角形中位线定理来解决问题.

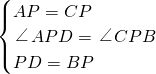 ,
, AD,EH∥AD,
AD,EH∥AD, AD,PG∥AD,HG=
AD,PG∥AD,HG= AC,
AC,
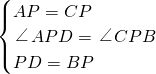 ,
, AD,EH∥AD,
AD,EH∥AD, FG,PG∥AD,HG=
FG,PG∥AD,HG= AC,
AC,