
科目:初中数学 来源:不详 题型:解答题
 的图象与
的图象与 轴、
轴、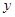 轴交于
轴交于 、
、 两点。
两点。
 、点
、点 的坐标和△
的坐标和△ 的面积。
的面积。 的长。
的长。 交于点
交于点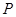 (
(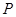 为一动点),把△
为一动点),把△ 的面积分成2︰1两部分,求直线L的解析式。
的面积分成2︰1两部分,求直线L的解析式。 查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.(1,1) | B.(-1,1) | C.(-2,-2) | D.(2,-2) |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 (mg)与燃烧时间
(mg)与燃烧时间 (分钟)成正比例;燃烧后,
(分钟)成正比例;燃烧后, 与
与 成反比例(如图所示).现测得药物10分钟燃完,此时教室内每立方米空气含药量为8mg.据以上信息解答下列问题:
成反比例(如图所示).现测得药物10分钟燃完,此时教室内每立方米空气含药量为8mg.据以上信息解答下列问题: 与
与 的函数关系式;
的函数关系式;
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 km/h;④汽车自出发后3h~4.5h之间行驶的速度在逐渐减小.其中正确的说法是 .(填上所有正确的序号)
km/h;④汽车自出发后3h~4.5h之间行驶的速度在逐渐减小.其中正确的说法是 .(填上所有正确的序号) 
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 (k>0)和x轴上,已知点B1(1,1),B2(3,2), 则Bn的坐标是______________.
(k>0)和x轴上,已知点B1(1,1),B2(3,2), 则Bn的坐标是______________. 
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
A.(3,1)(1, ); ); | B.(1,3)( ,1); ,1); | C.(3,0)(0, ) ; ) ; | D.(0,3)( ,0) ,0) |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com