
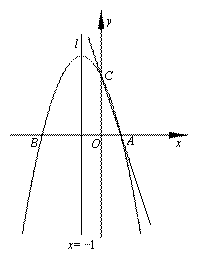
如图,已知直线 与x轴交于点A,与y轴交于点C,抛物线
与x轴交于点A,与y轴交于点C,抛物线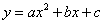 经过点A和点C,对称轴为直线l:
经过点A和点C,对称轴为直线l: ,该抛物线与x轴的另一个交点为B.
,该抛物线与x轴的另一个交点为B.
(1)求此抛物线的解析式;
(2)点P在直线l上,求出使△PAC的周长最小的点P的坐标;
(3)点M在此抛物线上,点N在y轴上,以A、B、M、N为顶点的四边形能否为平行四边形?若能,直接写出所有满足要求的点M的坐标;若不能,请说明理由.
 |
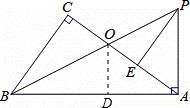
(1)证明:∵∠C=90°,∠BAP=90°
∴∠CBO+∠BOC=90°,∠ABP+∠APB=90°,
又∵∠CBO=∠ABP,
∴∠BOC=∠ABP,
∵∠BOC=∠AOP,
∴∠AOP=∠ABP,
∴AP=AO;
(2)证明:如图,过点O作OD⊥AB于D,
∵∠CBO=∠ABP,
∴CO=DO,
∵AE=OC,
∴AE=OD,
∵∠AOD+∠OAD=90°,∠PAE+∠OAD=90°,
∴∠AOD=∠PAE,
在△AOD和△PAE中,
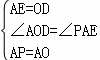 ,
,
∴△AOD≌△PAE(SAS),
∴∠AEP=∠ADO=90°
∴PE⊥AO;
(3)解:设AE=OC=3k,
∵AE=AC,∴AC=8k,
∴OE=AC﹣AE﹣OC=2k,
∴OA=OE+AE=5k.
由(1)可知,AP=AO=5k.
如图,过点O作OD⊥AB于点D,
∵∠CBO=∠ABP,∴OD=OC=3k.
在Rt△AOD中,AD=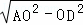 =
= =4k.
=4k.
∴BD=AB﹣AD=10﹣4k.
∵OD∥AP,
∴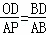 ,即
,即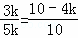
∵AB=10,PE=AD,
∴PE=AD=4K,BD=AB﹣AD=10﹣4k,
由∠CBO=∠ABP,根据轴对称BC=BD=10﹣4k,
∵∠BOC=∠EOP,∠C=∠PEO=90°,
∴△BCO∽△PEO,
∴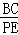 =
=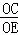 ,即
,即 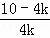 =
=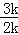 ,
,
解得k=1.
∴BD=10﹣4k=6,OD=3k=3,
在Rt△BDO中,由勾股定理得:
BO=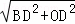 =
=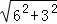 =3
=3 .
.


科目:初中数学 来源: 题型:
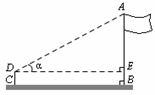
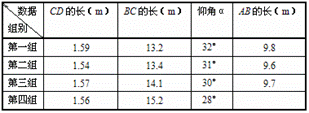
某校九年级四个数学活动小组参加测量操场旗杆高度的综合时间活动,如图是四个小组在不同位置测量后绘制的示意图,用测角仪测得旗杆顶端A的仰角级记为α,CD为测角仪的高,测角仪CD的底部C处与旗杆的底部B处之间的距离记为CB,四个小组测量和计算数据如下表所示:
(第21题)
(1)利用第四组学生测量的数据,求旗杆AB的高度(精确到0.1m);
(2)四组学生测量旗杆高度的平均值为 m(精确到0.1m).
查看答案和解析>>
科目:初中数学 来源: 题型:
关于x的一元二次方程x2+2(m﹣1)x+m2=0的两个实数根分别为x1,x2,且x1+x2>0,x1x2>0,则m的取值范围是( )
|
| A. | m≤ | B. | m≤ | C. | m<1 | D. | m<1且m≠0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com