练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】某种商品每件的标价是330元，按标价的八折销售时，仍可获利10%，则这种商品每件的进价为( )
    A.240元
    B.250元
    C.280元
    D.300元

    【答案】A
    【解析】解：设这种商品每件的进价为x元，

    由题意得：330×0.8﹣x=10%x，

    解得：x=240，即这种商品每件的进价为240元．
    故A符合题意.

    故答案为：A．

    设这种商品每件的进价为x元，根据售价-进价=利润(利润=进价 ×利润率)列方程求解.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，△ABC的三个顶点坐标为A（﹣3，4），B（﹣4，2），C（﹣2，1），

    △ABC绕原点顺时针旋转90°，得到△A1B1C1，△A1B1C1向左平移2个单位，再向下平移5个单

    位得到△A2B2C2．

    （1）画出△A1B1Cl和△A2B2C2；

    （2）P（a，b）是△ABC的AC边上一点，△ABC经旋转、平移后点P的对应点分别为P1、P2，请

    写出点P1、P2的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】心理学家研究发现，一般情况下，一节课40分钟中，学生的注意力随教师讲课的变化而变化．开始上课时，学生的注意力逐步增强，中间有一段时间学生的注意力保持较为理想的稳定状态，随后学生的注意力开始分散．经过实验分析可知，学生的注意力指数y随时间x（分钟）的变化规律如下图所示（其中AB、BC分别为线段，CD为双曲线的一部分）：

    （1）求出线段AB，曲线CD的解析式，并写出自变量的取值范围；

    （2）开始上课后第五分钟时与第三十分钟时相比较，何时学生的注意力更集中？

    （3）一道数学竞赛题，需要讲19分钟，为了效果较好，要求学生的注意力指数最低达到36，那么经过适当安排，老师能否在学生注意力达到所需的状态下讲解完这道题目？

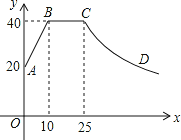
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图：点E是∠AOB的平分线上一点，ED⊥OA，EC⊥OB，垂足分别为C、D．

    求证：（1）OC=OD；

    （2）OE是线段CD的垂直平分线．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知a+b=﹣5，ab=6，则（a﹣b）2的值是 （ ）

    A. 25B. 13C. ﹣1D. 1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，以AB为直径的⊙O分别与BC，AC相交于点D，E，BD=CD，过点D作⊙O的切线交边AC于点F.

    (1)求证：DF⊥AC；

    (2)若⊙O的半径为5，∠CDF=30°，求的长(结果保留π)．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在美化校园的活动中，某兴趣小组想借助如图所示的直角墙角，墙DF足够长，墙DE长为12米，现用20米长的篱笆围成一个矩形花园ABCD，点C在墙DF上，点A在墙DE上，（篱笆只围AB，BC两边）．

    （1）如何才能围成矩形花园的面积为75m2？

    （2）能够围成面积为101m2的矩形花园吗？如能说明围法，如不能，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列调查中：
    ①了解一批袋装食品是否含有防腐剂；
    ②了解某班学生“50 米跑”的成绩；
    ③了解江苏卫视“非诚勿扰”节目的收视率；
    ④了解一批灯泡的使用寿命．
    适合用普查（全面调查）方式的是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，一次函数的图象分别与轴、轴交于点A、B，以线段AB为边在第一象限内作等腰Rt△ABC，∠BAC=90°．求过B、C两点直线的解析式．

    查看答案和解析>>

    同步练习册答案