
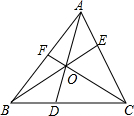
 如图,△ABC被分成了六部分,已知2BD=DC,EC=2AE,△AFO的面积为3平方厘米,则其它5部分的面积各是多少?
如图,△ABC被分成了六部分,已知2BD=DC,EC=2AE,△AFO的面积为3平方厘米,则其它5部分的面积各是多少? 分析 连接DE,根据已知条件得到$\frac{CD}{BD}=\frac{CE}{AE}=2$,推出DE∥AB,证得△DOE∽△AOB,△EOH∽△BOF,△ODH∽△OAF,得到比例式$\frac{OE}{OB}=\frac{OD}{AO}=\frac{DE}{AB}$=$\frac{2}{3}$,$\frac{HE}{BF}=\frac{OH}{OF}$,$\frac{DH}{AF}=\frac{OH}{OF}$,由等量代换得到$\frac{EH}{DH}=\frac{BF}{AF}$,由于△CHE∽△CFA,△CHD∽△CFB,同理:$\frac{EH}{AF}=\frac{DH}{BF}$,等量代换得到$\frac{BF}{AF}=\frac{AF}{BF}$,证得AF=BF,即可得到结论.
解答 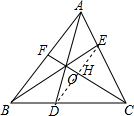 解:连接DE,
解:连接DE,
∵2BD=DC,EC=2AE,
∴$\frac{CD}{BD}=\frac{CE}{AE}=2$,
∴DE∥AB,
∴△DOE∽△AOB,△EOH∽△BOF,△ODH∽△OAF,
∴$\frac{OE}{OB}=\frac{OD}{AO}=\frac{DE}{AB}$=$\frac{2}{3}$,$\frac{HE}{BF}=\frac{OH}{OF}$,$\frac{DH}{AF}=\frac{OH}{OF}$,
∴$\frac{EH}{BF}=\frac{HD}{AF}$,
∴$\frac{EH}{DH}=\frac{BF}{AF}$,
∵DE∥AB,
∴△CHE∽△CFA,△CHD∽△CFB,
同理:$\frac{EH}{AF}=\frac{DH}{BF}$,
∴$\frac{EH}{DH}=\frac{AF}{BF}$,
∴$\frac{BF}{AF}=\frac{AF}{BF}$,
∴AF=BF,
∴S△BOF=S△AOF=3平方厘米,
∴S△BOD=S△AOE=$\frac{2}{3}$S△ABO=4平方厘米,
∴S△COD=S△COE=2△BDO=8平方厘米.
点评 本题考查了三角形的面积,相似三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.


科目:初中数学 来源: 题型:填空题
 如图,在各个手指间标记字母A,B,C,D.请按图中箭头所指方向(即A→B→C→D→C→B→A→B→C→…的方式)从A开始数连续的正整数1,2,3,4,….当字母C第2015次出现时,数到的数恰好是6045.
如图,在各个手指间标记字母A,B,C,D.请按图中箭头所指方向(即A→B→C→D→C→B→A→B→C→…的方式)从A开始数连续的正整数1,2,3,4,….当字母C第2015次出现时,数到的数恰好是6045.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0)
如图,已知的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 重合 | B. | 平行或重合 | C. | 垂直 | D. | 相交但不垂直 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com