
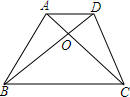
 如图,在梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,且AD:BC=1:2,则下列结论中,错误的是( )
如图,在梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,且AD:BC=1:2,则下列结论中,错误的是( )| A. | S△ABC=S△DBC | B. | S△AOB=S△COD | C. | 2S△AOD=S△BOC | D. | 2S△AOB=S△BOC |
分析 过A作AM⊥BC于M,过D作DN⊥BC于N,根据平行线间的距离相等得到AM=DN,根据三角形的面积得到S△ABC=S△DBC,故A正确;由于S△ABD-S△AOD=S△ACD-S△AOD,于是得到S△ABO=S△CDO,故B正确,通过△AOD∽△BCO,得到4S△AOD=S△BOC,故C错误;推出$\frac{AO}{CO}$=$\frac{AD}{BC}$=$\frac{1}{2}$,于是得到2S△AOB=S△BOC,故D正确;
解答 解:过A作AM⊥BC于M,过D作DN⊥BC于N,
∵AD∥BC,
∴AM=DN,
∵S△ABC=$\frac{1}{2}$•BC•AM,S△BCD=$\frac{1}{2}$•BC•DN,
∴S△ABC=S△DBC,故A正确;
同理:S△ABD=S△ACD,
∴S△ABD-S△AOD=S△ACD-S△AOD,
即S△ABO=S△CDO,故B正确,
∵AD∥BC,
∴△AOD∽△BCO,
∴$\frac{{S}_{△AOD}}{{S}_{△BOC}}$=($\frac{AD}{BC}$)2=$\frac{1}{4}$,
∴4S△AOD=S△BOC,故C错误;
∵△AOD∽△BCO,
∴$\frac{AO}{CO}$=$\frac{AD}{BC}$=$\frac{1}{2}$,
∴2S△AOB=S△BOC,故D正确;
故选C.
点评 本题考查了相似三角形的判定和性质,梯形的性质,弄清等底同高的三角形的面积相等,不同底但同高的三角形的面积的比等于底的比是解题的关键.


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案科目:初中数学 来源: 题型:选择题
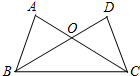 如图,下列条件中,不能证明△ABC≌△DCB的是( )
如图,下列条件中,不能证明△ABC≌△DCB的是( )| A. | AB=DC,AC=DB | B. | AB=DC,∠ABC=∠DCB | C. | AC=BD,∠A=∠D | D. | AB=DC,∠A=∠D |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
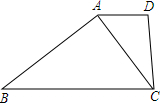 如图,AD∥BC,∠B=∠DCA.
如图,AD∥BC,∠B=∠DCA.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
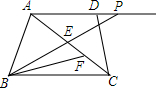 已知,如图,在梯形ABCD中,AD∥BC,BC=6,点P是射线AD上的点,BP交AC于点E,∠CBP的角平分线交AC于点F,且CF=$\frac{1}{3}$AC时.求AP+BP的值.
已知,如图,在梯形ABCD中,AD∥BC,BC=6,点P是射线AD上的点,BP交AC于点E,∠CBP的角平分线交AC于点F,且CF=$\frac{1}{3}$AC时.求AP+BP的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com