
分析 (1)由等腰Rt△ABC∽Rt△A′B′C′,相似比为3:1,根据相似比的定义可得:AB:A′B′=3:1,继而求得答案;
(2)由△A′B′C′是等腰直角三角形,利用三线合一的性质,可得△A′B′C′斜边A′B′上的高即是斜边A′B′上的中线,继而求得答案.
解答 解:(1)∵等腰Rt△ABC∽Rt△A′B′C′,相似比为3:1,
∴AB:A′B′=3:1,
∵Rt△ABC的斜边AB=12cm,
∴△A′B′C′斜边A′B′=4cm;
(2)∵△A′B′C′是等腰直角三角形,
∴△A′B′C′斜边A′B′上的高=△A′B′C′斜边A′B′上的中线,
∴△A′B′C′斜边A′B′上的高=2cm.
点评 此题考查了相似三角形的性质以及等腰直角三角形性质.注意理解相似比的意义是解此题的关键.


科目:初中数学 来源:2016-2017学年广东省东莞市堂星晨学校八年级3月月考数学试卷(解析版) 题型:解答题
某渔场计划购买甲、乙两种鱼苗共6000尾,甲种鱼苗每尾0.5元,乙种鱼苗每尾0.8元.相关资料表明:甲、乙两种鱼苗的成活率分别为90%和95%.
(1)若购买这批鱼苗共用了3600元,求甲、乙两种鱼苗各购买了多少尾?
(2)若购买这批鱼苗的钱不超过4200元,应如何选购鱼苗?
(3)若要使这批鱼苗的成活率不低于93%,且购买鱼苗的总费用最低,应如何选购鱼苗?
查看答案和解析>>
科目:初中数学 来源:2016-2017学年广西南宁市七年级下学期第一次月考数学试卷(解析版) 题型:解答题
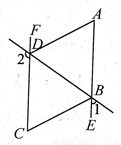
如图,∠1+∠2=180º,∠A=∠C,DA平分∠BDF。
(1)求证:AE∥FC.
(2)AD与BC的位置关系如何,为什么?
(3)证明:BC平分∠DBE.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com