
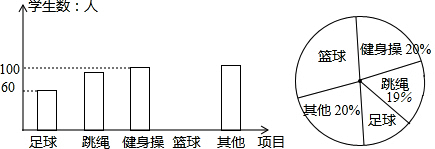
·ÖĪö £Ø1£©ÓĆ½”Éķ²ŁµÄČĖŹż³żŅŌĘäÕ¼×ÜČĖŹżµÄ°Ł·Ö±Č¼“æÉµĆ£»
£Ø2£©360”ć³ĖŅŌŃł±¾ÖŠ×ćĒņĖłÕ¼µÄ±ČĄż¼“æÉµĆ£»
£Ø3£©ĻČĒóµĆ×ćĒņČĖŹżĖłÕ¼±ČĄż£¬ŌŁøł¾Ż°Ł·Ö±ČÖ®ŗĶĪŖ1µĆ³öĄŗĒņµÄ°Ł·Ö±Č£¬×ÜČĖŹż³ĖŅŌĘäĖłÕ¼°Ł·Ö±ČĒóµĆČĖŹż¼“æɲ¹Č«Ķ¼ŠĪ£»
£Ø4£©×ÜČĖŹż18000³ĖŅŌŃł±¾ÖŠ×ćĒņµÄ°Ł·Ö±Č¼“æÉµĆ£®
½ā“š ½ā£ŗ£Ø1£©µ÷²éµÄ×ÜČĖŹżŹĒ£ŗ100”Ā20%=500£ØČĖ£©£»
£Ø2£©$\frac{60}{500}$”Į360”ć=30”ć£¬
“š£ŗÉČŠĪĶ³¼ĘĶ¼ÖŠ”°×īĻ²»¶×ćĒņŌĖ¶Æ”±µÄѧɜŹżĖł¶ŌÓ¦ÉČŠĪµÄŌ²ŠÄ½ĒĪŖ30”ć£»
£Ø3£©Ģß×ćĒņČĖŹżĖłÕ¼µÄ°Ł·Ö±ČŹĒ£ŗ$\frac{60}{500}$”Į100%=12%£¬
ĢߥŗĒņµÄČĖŹżŹĒ500”Į£Ø1-20%-19%-12%-20%£©=145£ØČĖ£©£¬
²¹Ķ¼ČēĻĀ£ŗ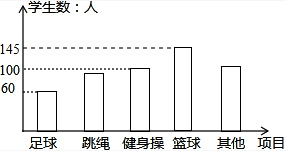
£Ø4£©øł¾ŻĢāŅāµĆ£ŗ18000”Į12%=2160£ØČĖ£©£®
“š£ŗČ«ŹŠ±¾½ģѧɜ֊”°×īĻ²»¶×ćĒņŌĖ¶Æ”±µÄѧɜŌ¼ÓŠ2160ČĖ£®
µćĘĄ ±¾Ģāæ¼²éµÄŹĒĢõŠĪĶ³¼ĘĶ¼ŗĶÉČŠĪĶ³¼ĘĶ¼µÄ×ŪŗĻŌĖÓĆ£¬¶Į¶®Ķ³¼ĘĶ¼£¬“Ó²»Ķ¬µÄĶ³¼ĘĶ¼ÖŠµĆµ½±ŲŅŖµÄŠÅĻ¢ŹĒ½ā¾öĪŹĢāµÄ¹Ų¼ü£®ĢõŠĪĶ³¼ĘĶ¼ÄÜĒ峞µŲ±ķŹ¾³öĆæøöĻīÄæµÄŹż¾Ż£»ÉČŠĪĶ³¼ĘĶ¼Ö±½Ó·“Ó³²æ·ÖÕ¼×ÜĢåµÄ°Ł·Ö±Č“󊔣®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | a£¼b£¼c£¼d | B£® | d£¼a£¼c£¼b | C£® | b£¼a£¼d£¼c | D£® | c£¼a£¼d£¼b |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com