
【题目】如图所示,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于
的图象交于![]() .
.
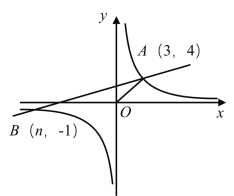
(1)求反比例函数和一次函数的解析式;
(2)在x轴上存在一点C,使![]() 为等腰三角形,求此时点C的坐标;
为等腰三角形,求此时点C的坐标;
(3)根据图象直接写出使一次函数的值大于反比例函数的值的x的取值范围.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ,
,![]() ,
,![]() ,
,![]() ;(3)-12<x<0或x>3
;(3)-12<x<0或x>3
【解析】
(1)因为反比例函数过A、B两点,所以可求其解析式和n的值,从而知B点坐标,进而求一次函数解析式;
(2)分三种情况:OA=OC,AO=AC,CA=CO,分别求解即可;
(3)根据图像得出一次函数图像在反比例函数图像上方时x的取值范围即可.
解:(1)把A(3,4)代入![]() ,
,
∴m=12,
∴反比例函数是![]() ;
;
把B(n,-1)代入![]() 得n=12.
得n=12.
把A(3,4)、B(-12,1)分别代入y=kx+b中:
得![]() ,
,
解得![]() ,
,
∴一次函数的解析式为![]() ;
;
(2)∵A(3,4),△AOC为等腰三角形,OA=![]() ,
,
分三种情况:
①当OA=OC时,OC=5,
此时点C的坐标为![]() ,
,![]() ;
;
②当AO=AC时,∵A(3,4),点C和点O关于过A点且垂直于x轴的直线对称,
此时点C的坐标为![]() ;
;
③当CA=CO时,点C在线段OA的垂直平分线上,
过A作AD⊥x轴,垂足为D,
由题意可得:OD=3,AD=4,AO=5,设OC=x,则AC=x,
在△ACD中,
![]() ,
,
解得:x=![]() ,
,
此时点C的坐标为![]() ;
;
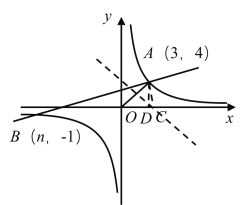
综上:点C的坐标为:![]() ,
,![]() ,
,![]() ,
,![]() ;
;
(3)由图得:
当一次函数图像在反比例函数图像上方时,
-12<x<0或x>3,
即使一次函数的值大于反比例函数的值的x的取值范围是:-12<x<0或x>3.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图所示,![]() 的顶点A在反比例函数
的顶点A在反比例函数![]() 的图像上,直线AB交y轴于点C,且点C的纵坐标为5,过点A、B分别作y轴的垂线AE、BF,垂足分别为点E、F,且
的图像上,直线AB交y轴于点C,且点C的纵坐标为5,过点A、B分别作y轴的垂线AE、BF,垂足分别为点E、F,且![]() .
.

(1)若点E为线段OC的中点,求k的值;
(2)若![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,其面积小于3.
,其面积小于3.
①求证:![]() ;
;
②把![]() 称为
称为![]() ,
,![]() 两点间的“ZJ距离”,记为
两点间的“ZJ距离”,记为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 和
和![]() 中,
中,![]() ,
,![]() 且
且![]() ,点
,点![]() 在
在![]() 的内部,连接
的内部,连接![]() ,
,![]() ,
,![]() 和
和![]() ,并且
,并且![]() .
.
(观察猜想)
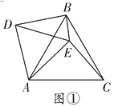
(1)如图①,当![]() 时,线段
时,线段![]() 与
与![]() 的数量关系为_____,线段
的数量关系为_____,线段![]() 的数量关系为_______________;
的数量关系为_______________;
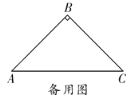
(探究证明)
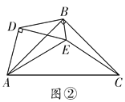
(2)如图②,当![]() 时,(1)中的结论是否依然成立?若成立,请给出证明,若不成立,请说明理由;
时,(1)中的结论是否依然成立?若成立,请给出证明,若不成立,请说明理由;
(拓展应用)
(3)在(2)的条件下,当点![]() 在线段
在线段![]() 上时,若
上时,若![]() ,请直接写出
,请直接写出![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小云在学习过程中遇到一个函数![]() .下面是小云对其探究的过程,请补充完整:
.下面是小云对其探究的过程,请补充完整:
(1)当![]() 时,对于函数
时,对于函数![]() ,即
,即![]() ,当
,当![]() 时,
时,![]() 随
随![]() 的增大而 ,且
的增大而 ,且![]() ;对于函数
;对于函数![]() ,当
,当![]() 时,
时,![]() 随
随![]() 的增大而 ,且
的增大而 ,且![]() ;结合上述分析,进一步探究发现,对于函数
;结合上述分析,进一步探究发现,对于函数![]() ,当
,当![]() 时,
时,![]() 随
随![]() 的增大而 .
的增大而 .
(2)当![]() 时,对于函数
时,对于函数![]() ,当
,当![]() 时,
时,![]() 与
与![]() 的几组对应值如下表:
的几组对应值如下表:
| 0 |
| 1 |
| 2 |
| 3 |
|
| 0 |
|
|
| 1 |
|
|
|
综合上表,进一步探究发现,当![]() 时,
时,![]() 随
随![]() 的增大而增大.在平面直角坐标系
的增大而增大.在平面直角坐标系![]() 中,画出当
中,画出当![]() 时的函数
时的函数![]() 的图象.
的图象.
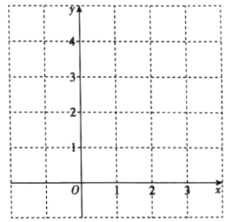
(3)过点(0,m)(![]() )作平行于
)作平行于![]() 轴的直线
轴的直线![]() ,结合(1)(2)的分析,解决问题:若直线
,结合(1)(2)的分析,解决问题:若直线![]() 与函数
与函数![]() 的图象有两个交点,则
的图象有两个交点,则![]() 的最大值是 .
的最大值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,![]() 均为等边三角形,边长分别为
均为等边三角形,边长分别为![]() ,B、C、D三点在同一条直线上,则下列结论正确的________________.(填序号)
,B、C、D三点在同一条直线上,则下列结论正确的________________.(填序号)
①![]() ②
②![]() ③
③![]() 为等边三角形 ④
为等边三角形 ④![]() ⑤CM平分
⑤CM平分![]()
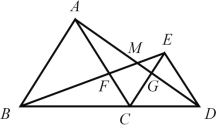
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知点A,对点A作如下变换:
第一步:作点A关于x轴的对称点A1;第二步:以O为位似中心,作线段OA1的位似图形OA2,且相似比![]() =q,则称A2是点A的对称位似点.
=q,则称A2是点A的对称位似点.
(1)若A(2,3),q=2,直接写出点A的对称位似点的坐标;
(2)已知直线l:y=kx-2,抛物线C:y=-![]() x2+mx-2(m>0).点N(
x2+mx-2(m>0).点N(![]() ,2k-2)在直线l上.
,2k-2)在直线l上.
①当k=![]() 时,判断E(1,-1)是否是点N的对称位似点,请说明理由;
时,判断E(1,-1)是否是点N的对称位似点,请说明理由;
②若直线l与抛物线C交于点M(x1,y1)(x1≠0),且点M不是抛物线的顶点,则点M的对称位似点是否可能仍在抛物线C上?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,给出下列结论:
①b2=4ac;②abc>0;③a>c;④4a﹣2b+c>0,其中正确的个数有( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某生产商存有1200千克![]() 产品,生产成本为150元/千克,售价为400元千克.因市场变化,准备低价一次性处理掉部分存货,所得货款全部用来生产
产品,生产成本为150元/千克,售价为400元千克.因市场变化,准备低价一次性处理掉部分存货,所得货款全部用来生产![]() 产品,
产品,![]() 产品售价为200元/千克.经市场调研发现,
产品售价为200元/千克.经市场调研发现,![]() 产品存货的处理价格
产品存货的处理价格![]() (元/千克)与处理数量
(元/千克)与处理数量![]() (千克)满足一次函数关系(
(千克)满足一次函数关系(![]() ),且得到表中数据.
),且得到表中数据.
|
|
200 | 350 |
400 | 300 |
(1)请求出处理价格![]() (元千克)与处理数量
(元千克)与处理数量![]() (千克)之间的函数关系;
(千克)之间的函数关系;
(2)若![]() 产品生产成本为100元千克,
产品生产成本为100元千克,![]() 产品处理数量为多少千克时,生产
产品处理数量为多少千克时,生产![]() 产品数量最多,最多是多少?
产品数量最多,最多是多少?
(3)由于改进技术,![]() 产品的生产成本降低到了
产品的生产成本降低到了![]() 元/千克,设全部产品全部售出,所得总利润为
元/千克,设全部产品全部售出,所得总利润为![]() (元),若
(元),若![]() 时,满足
时,满足![]() 随
随![]() 的增大而减小,求
的增大而减小,求![]() 的取值范围
的取值范围
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个边长都为![]() 的小正方形组成的网格中,小正方形的顶点叫做格点.线段
的小正方形组成的网格中,小正方形的顶点叫做格点.线段![]() 的端点
的端点![]() 均在格点上.
均在格点上.
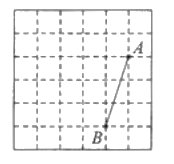
(1)线段![]() 的长度等于 ;
的长度等于 ;
(2)将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,在图中画出
,在图中画出![]() ,并连结
,并连结![]() .
.
(3)在线段![]() 上确定一点
上确定一点![]() 连结
连结![]() ,使得
,使得![]() 与
与![]() 的面积比为
的面积比为![]() .
.
说明:以上作图只用无刻度的直尺画图,保留画图痕迹,不写画法.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com