练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    设M＝x－y，其中x可取－1、2，y可取－1、－2、3．

    (1)求出M的所有等可能结果(用树状图或列表法求解)；

    (2)试求M是正值的概率．

    答案：
    解析：

    　　解：(1)

    　　5分

    　　(2)　8分


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    （11·兵团维吾尔）（10分）如图，在等腰梯形ABCD中，AD＝4，BC＝9，∠

    B＝45°．动点P从点B出发沿BC向点C运动，动点Q同时以相同速度从点C出发沿CD

    向点D运动，其中一个动点到达端点时，另一个动点也随之停止运动．

    （1）求AB的长；

    （2）设BP＝x，问当x为何值时△PCQ的面积最大，并求出最大值；

    （3）探究：在AB边上是否存在点M，使得四边形PCQM为菱形？请说明理由．

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    ）如图，在△ABC中，∠ABC和∠ACB的平分线相交于点O，过点O作EF∥BC交AB于E，交AC于F，过点O作OD⊥AC于D．下列四个结论：
    ①∠BOC＝90º＋∠A；    ②以E为圆心、BE为半径的圆与以F为圆心、CF为半径的圆外切；
    ③设OD＝m，AE＋AF＝n，则S△AEF＝mn； ④EF是△ABC的中位线．
    其中正确的结论是_____________．

    查看答案和解析>>

    科目：初中数学 来源：2012年人教新课标版中考综合模拟数学卷（4） 题型：填空题

    ）如图，在△ABC中，∠ABC和∠ACB的平分线相交于点O，过点O作EF∥BC交AB于E，交AC于F，过点O作OD⊥AC于D．下列四个结论：
    ①∠BOC＝90º＋∠A；    ②以E为圆心、BE为半径的圆与以F为圆心、CF为半径的圆外切；
    ③设OD＝m，AE＋AF＝n，则S△AEF＝mn； ④EF是△ABC的中位线．
    其中正确的结论是_____________．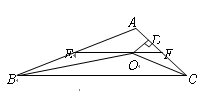

    查看答案和解析>>

    科目：初中数学 来源：2012-2013学年江苏省南京市鼓楼区中考二模数学试卷（解析版） 题型：解答题

    【提出问题】

    如图①，在梯形ABCD中，AD//BC，AC、BD交于点E，∠BEC＝n°，若AD＝a，BC＝b，则梯形ABCD的面积最大是多少？

    【探究过程】

    小明提出：可以从特殊情况开始探究，如图②，在梯形ABCD中，AD//BC，AC⊥BD，若AD＝3，BC＝7，则梯形ABCD的面积最大是多少？

    如图③，过点D做DE//AC交BC的延长线于点E，那么梯形ABCD的面积就等于△DBE的面积，求梯形ABCD的面积最大值就是求△DBE的面积最大值．如果设AC＝x，BD＝y，那么S△DBE＝xy．

    以下是几位同学的对话：

    A同学：因为y＝，所以S△DBE＝x，求这个函数的最大值即可．

    B同学：我们知道x2＋y2＝100，借助完全平方公式可求S△DBE＝xy的最大值

    C同学：△DBE是直角三角形，底BE＝10，只要高最大，S△DBE就最大，我们先将所有满足BE＝10的直角△DBE都找出来，然后在其中寻找高最大的△DBE即可．

    （1）请选择A同学或者B同学的方法，完成解题过程．

    （2）请帮C同学在图③中画出所有满足条件的点D，并标出使△DBE面积最大的点D1．（保留作图痕迹，可适当说明画图过程）

    【解决问题】

    根据对特殊情况的探究经验，请在图①中画出面积最大的梯形ABCD的顶点D1，并直接写出梯形ABCD面积的最大值．

     

    查看答案和解析>>

    同步练习册答案