
【题目】如图1,已知△ABC中,AB=10cm,AC=8cm,BC=6cm.如果点P由B出发沿BA方向点A匀速运动,同时点Q由A出发沿AC方向向点C匀速运动,它们的速度均为2cm/s.连接PQ,设运动的时间为t(单位:s)(0≤t≤4).解答下列问题:

(1)当t为何值时,PQ∥BC.
(2)设△AQP面积为S(单位:cm2),当t为何值时,S取得最大值,并求出最大值.
(3)是否存在某时刻t,使线段PQ恰好把△ABC的面积平分?若存在,求出此时t的值;若不存在,请说明理由.
(4)如图2,把△AQP沿AP翻折,得到四边形AQPQ′.那么是否存在某时刻t,使四边形AQPQ′为菱形?若存在,求出此时菱形的面积;若不存在,请说明理由.
【答案】(1)![]() s(2)当t=
s(2)当t=![]() s时,S取得最大值,最大值为
s时,S取得最大值,最大值为![]() cm2(3)不存在。理由见解析(4)存在,
cm2(3)不存在。理由见解析(4)存在,![]() cm2
cm2
【解析】
解:∵AB=10cm,AC=8cm,BC=6cm,
∴由勾股定理逆定理得△ABC为直角三角形,∠C为直角。
(1)BP=2t,则AP=10﹣2t.
若PQ∥BC,则![]() ,即
,即![]() ,解得
,解得![]() 。
。
∴当![]() s时,PQ∥BC。
s时,PQ∥BC。
(2)如图1所示,过P点作PD⊥AC于点D。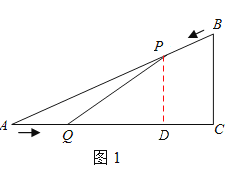
则PD∥BC,∴△APD∽△ABC。
∴![]() ,即
,即![]() ,解得
,解得![]() 。
。
∴S=![]() ×AQ×PD=
×AQ×PD=![]() ×2t×(
×2t×(![]() )
)
![]() 。
。
∴当t=![]() s时,S取得最大值,最大值为
s时,S取得最大值,最大值为![]() cm2。
cm2。
(3)不存在。理由如下:
假设存在某时刻t,使线段PQ恰好把△ABC的面积平分,
则有S△AQP=![]() S△ABC,而S△ABC=
S△ABC,而S△ABC=![]() ACBC=24,∴此时S△AQP=12。
ACBC=24,∴此时S△AQP=12。
由(2)可知,S△AQP=![]() ,∴
,∴![]() =12,化简得:t2﹣5t+10=0。
=12,化简得:t2﹣5t+10=0。
∵△=(﹣5)2﹣4×1×10=﹣15<0,此方程无解,
∴不存在某时刻t,使线段PQ恰好把△ABC的面积平分。
(4)存在。
假设存在时刻t,使四边形AQPQ′为菱形,
则有AQ=PQ=BP=2t。
如图2所示,过P点作PD⊥AC于点D,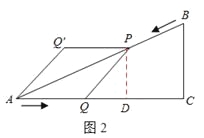
则有PD∥BC,
∴△APD∽△ABC。
∴![]() ,即
,即![]() 。
。
解得:PD=![]() ,AD=
,AD=![]() ,
,
∴QD=AD﹣AQ=![]() 。
。
在Rt△PQD中,由勾股定理得:QD2+PD2=PQ2,即(![]() )2+(
)2+(![]() )2=(2t)2,
)2=(2t)2,
化简得:13t2﹣90t+125=0,解得:t1=5,t2=![]() 。
。
∵t=5s时,AQ=10cm>AC,不符合题意,舍去,∴t=![]() 。
。
由(2)可知,S△AQP=![]()
∴S菱形AQPQ′=2S△AQP=2×(![]() )=2×[﹣
)=2×[﹣![]() ×(
×(![]() )2+6×
)2+6×![]() ]=
]=![]() 。
。
∴存在时刻t=![]() ,使四边形AQPQ′为菱形,此时菱形的面积为
,使四边形AQPQ′为菱形,此时菱形的面积为![]() cm2。
cm2。
(1)由PQ∥BC时的比例线段关系,列一元一次方程求解。
(2)如图1所示,过P点作PD⊥AC于点D,得△APD∽△ABC,由比例线段,求得PD,从而可以得到S的表达式,然后利用二次函数的极值求得S的最大值。
(3)利用(2)中求得的△AQP的面积表达式,再由线段PQ恰好把△ABC的面积平分,列出一元二次方程;由于此一元二次方程的判别式小于0,则可以得出结论:不存在这样的某时刻t,使线段PQ恰好把△ABC的面积平分。
(4)根据菱形的性质及相似三角形比例线段关系,求得PQ、QD和PD的长度;然后在Rt△PQD中,求得时间t的值;最后求菱形的面积,值得注意的是菱形的面积等于△AQP面积的2倍,从而可以利用(2)中△AQP面积的表达式,这样可以化简计算。


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】某学校举行一场知识竞赛活动,竞赛共有4小题,每小题5分,答对给5分,答错或不答给0分,在该学校随机抽取若干同学参加比赛,成绩被制成不完整的统计表如下.
成绩 | 人数 | 百分比 |
0 | ||
5 |
| |
10 | 5 | |
15 |
| |
20 | 5 |
|
根据表中已有的信息,下列结论正确的是![]()
![]()
A. 共有40名同学参加知识竞赛
B. 抽到的同学参加知识竞赛的平均成绩为10分
C. 已知该校共有800名学生,若都参加竞赛,得0分的估计有100人
D. 抽到同学参加知识竞赛成绩的中位数为15分
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABOC中,∠ABO=120°,它的一个顶点C在反比例函数y=![]() 的图象上,若将菱形向下平移2个单位,点A恰好落在函数图象上,则该反比函数的表达式为( )
的图象上,若将菱形向下平移2个单位,点A恰好落在函数图象上,则该反比函数的表达式为( )

A. y=﹣![]() B. y=﹣
B. y=﹣![]() C. y=﹣
C. y=﹣![]() D. y=-
D. y=-![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙三位运动员在相同条件下各射靶10次,每次射靶的成绩如下:
甲:9,10,8,5,7,8,10,8,8,7;
乙:5,7,8,7,8,9,7,9,10,10;
丙:7,6,8,5,4,7,6,3,9,5.
(1)根据以上数据求出表中a,b,c的值;
平均数 | 中位数 | 方差 | |
甲 | 8 | 8 | b |
乙 | a | 8 | 2.2 |
丙 | 6 | c | 3 |
(2)根据表中数据分析,哪位运动员的成绩最稳定,并简要说明理由;
(3)比赛时三人依次出场,顺序由抽签方式决定,用列举法求甲、乙相邻出场的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,两个含有30°角的完全相同的三角板ABC和DEF沿直线l滑动,下列说法错误的是( )
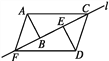
A. 四边形ACDF是平行四边形 B. 当点E为BC中点时,四边形ACDF是矩形
C. 当点B与点E重合时,四边形ACDF是菱形 D. 四边形ACDF不可能是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=3,点E,F分别在CD,AD上,CE=DF,BE,CF相交于点G.若图中阴影部分的面积与正方形ABCD的面积之比为2:3,则△BCG的周长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正六边形ABCDEF中,对角线AE与BF相交于点M,BD与CE相交于点N.
(1)求证:AE=FB;
(2)在不添加任何辅助线的情况下,请直接写出所有与△ABM全等的三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中装有大小和形状相同的3个红球和2个白球,把它们充分搅匀.
(1)“从中任意抽取1个球不是红球就是白球”是 事件,“从中任意抽取1个球是黑球”是 事件;
(2)从中任意抽取1个球恰好是红球的概率是 ;
(3)学校决定在甲、乙两名同学中选取一名作为学生代表发言,制定如下规则:从盒子中任取两个球,若两球同色,则选甲;若两球异色,则选乙.你认为这个规则公平吗?请用列表法或画树状图法加以说明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com