A
分析:先根据题意得出△ABC是等腰三角形,再根据等腰三角形的性质得出∠C=∠ABC=72°,由BD是∠ABC的平分线可知,
∠ABD=∠A=36°故可得出△ABD是等腰三角形,由DE∥AB,可知∠1=∠ABD=∠2=36°,故△BDE是等腰三角形;DE∥AB可得出BD=BC,△BDC是等腰三角形;同理即可得出△DEF、△CEF、△CDE是等腰三角形.
解答:
解:∵AB=AC,
∴△ABC是等腰三角形;
∵∠A=36°,
∴∠C=∠ABC=

=

=72°,
∵BD是∠ABC的平分线,
∴∠ABD=∠2=
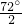
=36°,
∴∠ABD=∠A=36°,
∴AD=BD,
∴△ABD是等腰三角形;
∵DE∥AB,
∴∠1=∠ABD=∠2=36°,
∴△BDE是等腰三角形;
∵DE∥AB,
∴∠3=∠A=36°,
∴∠1+∠3=72°,
∴∠C=180°-∠2-(∠1+∠3)=180°-36°-72°=72°,
∴BD=BC,
∴△BDC是等腰三角形;
∵EF∥BD,
∴∠6=∠1=36°,
∴∠3=∠6=36°,
∴DF=EF,
∴△DEF是等腰三角形;
∵EF∥DE,
∴∠4=∠1+∠3=72°,
∵∠C=72°,
∴∠5=180°-∠C-∠4=180°-72°-72°=36°,
∴△CEF是等腰三角形;
∵∠C=72°,∠5+∠6=72°,
∴CD=DE,
∴△CDE是等腰三角形.
故图中的等腰三角形有:△ABC,△ABD,△BDC,△DEC,△BDE,△DEF,△EFC共7个.
故选A.
点评:本题考查的是等腰三角形的判定与性质,平行线的性质,解答此类题目时往往用到三角形的内角和是180°这一隐藏条件.

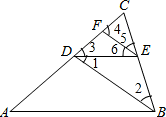
 如图,在△ABC中,AB=AC,∠A=36°,BD为∠ABC的平分线,DE∥AB,EF∥BD,则图中等腰三角形共有
如图,在△ABC中,AB=AC,∠A=36°,BD为∠ABC的平分线,DE∥AB,EF∥BD,则图中等腰三角形共有 解:∵AB=AC,
解:∵AB=AC, =
= =72°,
=72°,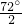 =36°,
=36°,

 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为