考点:根与系数的关系,二次根式的化简求值
专题:计算题,方程思想
分析:根据已知条件“(a+1)2=3-3(a+1),3(b+1)=3-(b+1)2”求出a+1、b+1是关于x的方程x2+3x-3=0的两个根,
然后再根据根与系数的关系求得a+b=-5,ab=1;最后将其代入化简后的二次根式并求值即可.
解答:解:∵(a+1)
2=3-3(a+1),3(b+1)=3-(b+1)
2.
∴(a+1)
2+3(a+1)-3=0,(b+1)
2+3(b+1)-3=0,
显然,a+1、b+1是关于x的方程x
2+3x-3=0的两个根,
∴x
1+x
2=-3,即a+1+b+1=-3,
∴a+b=-5;
x
1•x
2=-3,即(a+1)(b+1)=ab+(a+b)+1=-3,
∴ab=1,
∴a=
,b=
;
∴
b+a,
=b|b|+a|a|,
=-[(b+a)
2-2ab],
=-25+2,
=-23;
故答案是:-23.
点评:本题考查了根与系数的关系、二次根式的化简求值.解答此题时,如果先根据已知条件求得a、b的值,然后将其代入所求的代数式求值,那计算过程是相当的繁琐.根据已知条件“(a+1)2=3-3(a+1),3(b+1)=3-(b+1)2”可以知,“(a+1)2+3(a+1)-3=0,(b+1)2+3(b+1)-3=0”,仔细观察这两个等式可知:a+1、b+1是关于x的方程x2+3x-3=0的两个根.然后再根据一元二次方程的根与系数的关系求得a与b的数量关系,并将其代入所求的代数式求值.这样,计算会变得简单多了.



 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案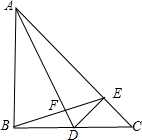 已知如图,△ABC中,∠ABC=90°,AB=BC,D是BC边上一点,DE⊥AC于E,连BE交AD与F.
已知如图,△ABC中,∠ABC=90°,AB=BC,D是BC边上一点,DE⊥AC于E,连BE交AD与F.