
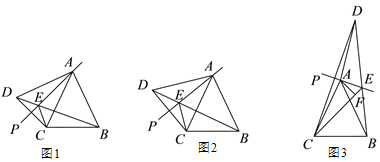
【题目】在△ABC 中,AB=AC,∠CAB=50°.在△ABC 的外侧作直线 AP,作 点 C 关于直线 AP 的对称点 D,连接 BD,CD,AD,其中 BD 交直线 AP 于点 E.
(1)如图 1,与 AD 相等的线段是_____;
(2)如图 2,若∠PAC=20°,求∠BDC 的度数;
(3)如图 3,当 65°<∠PAC<130°时,作 AF⊥CE 于点 F,若 EF=1,BE=5,求 DE 的长.
【答案】(1)AC,AB;(2)25°;(3)7.
【解析】
(1)易得与 AD 相等的线段是 AC,AB;
(2)由点 C 与点 D 关于直线 AP 对称可得∠DAP=∠CAP=20°,∠DAC=40°∠ADC=70°,由(1)AD=AB,可得△ADB为等腰直角三角形,∠ADB=45°,可得∠BDC 的度数;
(3) 在 CE 上截取 GF=EF,连接 AG,点 C 与点 D 关于直线 AP 对称可得:AD=AC,∠ADE=∠ACE,可证的△ACG≌△ABE,得DE=CE=CG+2EF=BE+2EF=7.
(1)如图 1,与 AD 相等的线段是 AC,AB;

(2)∵点 C 与点 D 关于直线 AP 对称,
∴AD=AC,∠DAP=∠CAP=20°,
∴∠DAC=40°,∠ADC=70°又∠CAB=50°,
∴∠DAB=90°,
∵AC=AB,
∴AD=AB,
∴∠ADB=45°,
∴∠BDC=∠ADC-∠ADB=25°;
(3)在 CE 上截取 GF=EF,连接 AG,

∵点 C 与点 D 关于直线 AP 对称,
∴AD=AC,∠ADE=∠ACE,
∵AD=AC=AB,
∴∠ADB=∠ABD,
∴∠ACE=∠ABD,
∵AF⊥CE,GF=EF,
∴AG=AE,
∴∠AGE=∠AEB,
∵∠AED=∠AEG,
∴∠AGE=∠AED,
∴∠AGC=∠AEB
在△ACG 和△ABE 中,
ACG ABD,AGC AEB, AC AB,
∴△ACG≌△ABE(AAS),
∴BE=CG,
∵BE=5,CE=1,
∴DE=CE=CG+2EF=BE+2EF=7.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD 相交于点O,∠AOD=3∠BOD+20°.
(1)求∠BOD的度数;
(2)以O为端点引射线OE,OF ,射线OE平分∠BOD,且∠EOF= 90°,求∠BOF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知OA⊥OB,∠AOD=∠BOC由此判定OC⊥OD,下面是推理过程,请填空.

解:∵OA⊥OB(已知)
所以_____=90°(________)
因为_____=∠AOD-∠AOC,____=∠BOC-∠AOC,∠AOD=∠BOC,
所以______=_____(等量代换)
所以______=90°
所以OC⊥OD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,PB、PC分别是⊙O的切线,切点为B、C,PC、BA的延长线交于点D,DE⊥PO,交PO的延长线于点E. 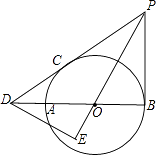
(1)求证:∠DPO=∠EDB;
(2)若PB=3,DB=4,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育中考前,抽样调查了九年级学生的“1分钟跳绳”成绩,并绘制成了下面的频数分布直方图(每小组含最小值,不含最大值)和扇形图. 
(1)补全频数分布直方图;
(2)扇形图中m=;
(3)若“1分钟跳绳”成绩大于或等于140次为优秀,则估计全市九年级5900名学生中“1分钟跳绳”成绩为优秀的大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求一个正数的算术平方根,有些数可以直接求得,如![]() ;有些数则不能直接求得,如
;有些数则不能直接求得,如![]() ,除通过计算器可以求得外,还可以通过一组数的内在联系,运用规律求得,观察下表:
,除通过计算器可以求得外,还可以通过一组数的内在联系,运用规律求得,观察下表:
n | 0.09 | 9 | 900 | 90000 | … |
| 0.3 | 3 | 30 | 300 | … |
(1)根据表中的规律,可以求得![]() ____,
____,![]() ____;
____;
(2)根据表中的规律,还可以由![]() ≈1.435,求得
≈1.435,求得![]() ≈____,
≈____,![]() ≈____,
≈____,![]() ≈____.
≈____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P(a,b),若点P′的坐标为(a+kb,ka+b)(其中k为常数,且k≠0),则称点P′为点P的“k属派生点”.
例如:P(1,4)的“2属派生点”为P′(1+2×4,2×1+4),即P′(9,6).
(1)点P(-1,6)的“2属派生点”P′的坐标为_____________;
(2)若点P的“3属派生点”P′的坐标为(6,2),则点P的坐标___________;
(3)若点P在x轴的正半轴上,点P的“k属派生点”为P′点,且线段PP′的长度为线段OP长度的2倍,求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com