
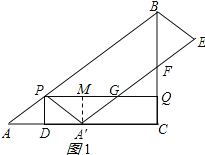
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=8cm,AB=10cm.点P从点A出发,以5cm/s的速度从点A运动到终点B;同时,点Q从点C出发,以3cm/s的速度从点C运动到终点B,连结PQ;过点P作PD⊥AC交AC于点D,将△APD沿PD翻折得到△A′PD,以A′P和PB为邻边作A′PBE,A′E交射线BC于点F,交射线PQ于点G.设A′PBE与四边形PDCQ重叠部分图形的面积为Scm2,点P的运动时间为ts.
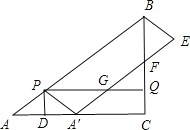
(1)当t为 时,点A′与点C重合;
(2)求S与t的函数关系式;
(3)请直接写出当射线PQ将A′PBE分成的两部分图形的面积之比是1:3时t的值.
【答案】(1)1s;(2)s=﹣42t2+72t﹣24.(3)见解析
【解析】
试题分析:(1)证明△ADP∽△ACB,从而可得AD=4t,由折叠可得AA′=2AD=8t,由点A′与点C重合可得8t=8,从而可以求出t的值.
(2)分三种情况讨论:①当0<t≤![]() 时,过点 A′作A′M⊥PG于M,证明△BPQ∽△BAC.得出∠BQP=∠BCA.证出PQ∥AC,证明四边形APGA′是平行四边形,得出PG=AA′=8t,即可得出结果;
时,过点 A′作A′M⊥PG于M,证明△BPQ∽△BAC.得出∠BQP=∠BCA.证出PQ∥AC,证明四边形APGA′是平行四边形,得出PG=AA′=8t,即可得出结果;
②当![]() <t≤1时,过点 A′作A′M⊥PG于M,则有A′M=QC=3t,PQ=DC=8﹣4t,PG=AA′=8t,QG=PG﹣PQ=12t﹣8,QF=9t﹣6.由S=S△A′PG﹣S△GQF,即可得出结果.
<t≤1时,过点 A′作A′M⊥PG于M,则有A′M=QC=3t,PQ=DC=8﹣4t,PG=AA′=8t,QG=PG﹣PQ=12t﹣8,QF=9t﹣6.由S=S△A′PG﹣S△GQF,即可得出结果.
③当1<t<2时,证出PB=PS.得出BQ=SQ.因此SQ=6﹣3t,即可得出结果.
(3)可分①S△A′PG:S四边形PBEG=1:3,如图4,②S△BPN:S四边形PNEA′=1:3,如图5,两种情况进行讨论,就可解决问题.
解:(1)根据题意得:PA′=PA=5t,CQ=3t,AD=A′D.
∵∠ACB=90°,AC=8,AB=10,
∴BC=6.
∵∠ADP=∠ACB=90°,
∴PD∥BC.
∴△ADP∽△ACB.
∴![]() =
=![]() =
=![]() .
.
∴![]() =
=![]() =
=![]() .
.
∴AD=4t,PD=3t.
∴AA′=2AD=8t.
当点A′与点C重合时,AA′=AC.
∴8t=8.
∴t=1;
故答案为:1s.
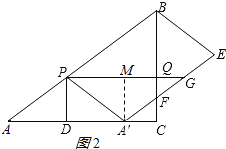
(2)①当0<t≤![]() 时,
时,
过点 A′作A′M⊥PG,垂足为M,如图1所示,
则有A′M=CQ=3t.
∵![]() =
=![]() =
=![]() ,
,![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∵∠PBQ=∠ABC,
∴△BPQ∽△BAC.
∴∠BQP=∠BCA.
∴PQ∥AC.
∵AP∥A′G.
∴四边形APGA′是平行四边形.
∴PG=AA′=8t.
∴S=S△A′PG=![]() PGA′M
PGA′M
=![]() ×8t×3t=12t2.
×8t×3t=12t2.
②当![]() <t≤1时,
<t≤1时,
过点 A′作A′M⊥PG,垂足为M,如图2所示,
则有A′M=QC=3t,PQ=DC=8﹣4t,PG=AA′=8t,QG=PG﹣PQ=12t﹣8,QF=9t﹣6.
∴S=S△A′PG﹣S△GQF
=![]() PGA′M﹣
PGA′M﹣![]() QGQF
QGQF
=![]() ×8t×3t﹣
×8t×3t﹣![]() ×(12t﹣8)×(9t﹣6)
×(12t﹣8)×(9t﹣6)
=﹣42t2+72t﹣24.
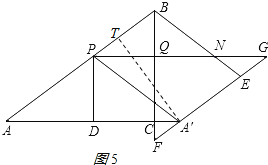
③当1<t<2时,如图3所示,
∵PQ∥AC,PA=PA′
∴∠BPQ=∠PAA′,∠QPA′=∠PA′A,∠PAA′=∠PA′A.
∴∠BPQ=∠QPA′.
∵∠PQB=∠PQS=90°,
∴∠PBQ=∠PSQ.
∴PB=PS.
∴BQ=SQ.
∴SQ=6﹣3t.
∴S=S△PQS=![]() PQQS=
PQQS=![]() ×(8﹣4t)×(6﹣3t)=6t2﹣24t+24.
×(8﹣4t)×(6﹣3t)=6t2﹣24t+24.
综上所述:当0<t≤![]() 时,S=12t2;
时,S=12t2;
当![]() <t≤1时,S=﹣42t2+72t﹣24;
<t≤1时,S=﹣42t2+72t﹣24;
当1<t<2时,S=6t2﹣24t+24.
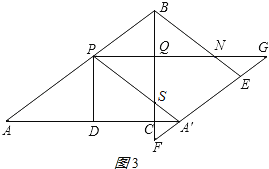
(3)①若S△A′PG:S四边形PBEG=1:3,
过点A′作A′M⊥PG,垂足为M,过点A′作A′T⊥PB,垂足为T,如图4所示,
则有A′M=PD=QC=3t,PG=AA′=8t.
∴S△A′PG=![]() ×8t×3t=12t2.
×8t×3t=12t2.
∵S△APA′=![]() APA′T=
APA′T=![]() AA′PD,
AA′PD,
∴A′T=![]() =
=![]() =
=![]() t.
t.
∴SPBEA′=PBA′T=(10﹣5t)×![]() t=24t(2﹣t).
t=24t(2﹣t).
∵S△A′PG:S四边形PBEG=1:3,
∴S△A′PG=![]() ×SPBEA′.
×SPBEA′.
∴12t2=![]() ×24t(2﹣t).
×24t(2﹣t).
∵t>0,
∴t=![]() .
.
②若S△BPN:S四边形PNEA′=1:3,如图5所示,
同理可得:∠BPQ=∠A′PQ,BQ=6﹣3t,PQ=8﹣4t,平行四边形PBEA′的面积=24t(2﹣t).
∵四边形PBEA′是平行四边形,
∴BE∥PA′.
∴∠BNP=∠NPA′.
∴∠BPN=∠BNP.
∴BP=BN.
∵∠BQP=∠BQN=90°,
∴PQ=NQ.
∴S△BPN=![]() PNBQ=PQBQ
PNBQ=PQBQ
=(8﹣4t)×(6﹣3t).
∵S△BPN:S四边形PNEA′=1:3,
∴S△BPN=![]() ×SPBEA′.
×SPBEA′.
∴(8﹣4t)×(6﹣3t)=![]() ×24t(2﹣t).
×24t(2﹣t).
∴(8﹣4t)×(6﹣3t)=![]() ×24t(2﹣t).
×24t(2﹣t).
∵t<2,
∴t=![]() .
.
综上所述:当射线PQ将A′PBE分成的两部分图形的面积之比是1:3时,t的值为![]() 秒或
秒或![]() 秒.
秒.



科目:初中数学 来源: 题型:
【题目】一个长为19cm,宽为18cm的长方形,如果把这个长方形分成若干个正方形要求正方形的边长为正整数,那么该长方形最少可分成正方形的个数( )
A. 5个 B. 6个 C. 7个 D. 8个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y1=![]() x与双曲线y2=
x与双曲线y2=![]() (k>0)交于A、B两点,且点A的横坐标为4.
(k>0)交于A、B两点,且点A的横坐标为4.

(1)k的值为 ;当x的取值范围为 时,y1>y2;
(2)若双曲线y2=![]() (k>0)上一点C的纵坐标为8,求△AOC的面积.
(k>0)上一点C的纵坐标为8,求△AOC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某车间有26名工人,每人每天可以生产800个螺钉或1000个螺母,1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母刚好配套.设安排x名工人生产螺钉,则下面所列方程正确的是( )
A.2×1000(26﹣x)=800x B.1000(13﹣x)=800x
C.1000(26﹣x)=2×800x D.1000(26﹣x)=800x
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com