
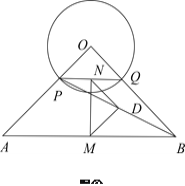
【题目】如图本题图①,在等腰Rt![]() 中,
中,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上一点,以
上一点,以![]() 为半径作
为半径作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() ,线段
,线段![]() 、
、![]() 、
、![]() 的中点分别为
的中点分别为![]() 、
、![]() 、
、![]() .
.
(1)试探究![]() 是什么特殊三角形?说明理由;
是什么特殊三角形?说明理由;
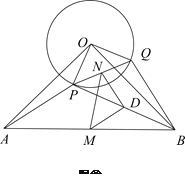
(2)将![]() 绕点
绕点![]() 逆时针方向旋转到图②的位置,上述结论是否成立?并证明结论;
逆时针方向旋转到图②的位置,上述结论是否成立?并证明结论;
(3)若![]() ,把
,把![]() 绕点
绕点![]() 在平面内自由旋转,求
在平面内自由旋转,求![]() 的面积y的最大值与最小值的差.
的面积y的最大值与最小值的差.
【答案】(1)![]() 为等腰直角三角形;(2)
为等腰直角三角形;(2)![]() 仍然为等腰直角三角形;(3)
仍然为等腰直角三角形;(3)![]() 的最大值与最小值的差为:
的最大值与最小值的差为:![]()
【解析】分析:(1)由OA=OB,OP=OQ可得AP=BQ,再利用三角形的中位线可得△DMN是等腰直角三角形;
(2)由旋转的性质得∠AOP=∠BOQ,从而可证△AOP≌△BOQ,由三角形中位线的性质可得DM=DN,根据平行线的性质和三角形内角和可证∠MDN=90°,从而结论得证;
(3)如图,设⊙![]() 交
交![]() 于点
于点![]() ,交
,交![]() 延长线于点
延长线于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() .由三角形三边的关系得
.由三角形三边的关系得![]() ,
,![]() ,由三角形的面积公式得
,由三角形的面积公式得![]() ,从而可求出y的最大值和最小值,然后相减即可.
,从而可求出y的最大值和最小值,然后相减即可.
详解:(1)![]() 为等腰直角三角形
为等腰直角三角形
![]()
![]() 分别为
分别为![]() 的中点,
的中点,
![]()
![]() 且
且![]()
同理:![]()
![]()
![]()
![]()
![]() .
.
又![]()
![]()
![]()
![]() 即
即![]() 为等腰直角三角形.
为等腰直角三角形.
(2)如图,![]() 仍然为等腰直角三角形.
仍然为等腰直角三角形.
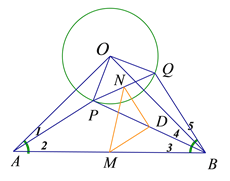
证明:由旋转的性质,![]() .
.
![]()
![]()
![]()
![]() ≌
≌![]() ,
,
![]()
![]() .
.
![]()
![]() 分别为
分别为![]() 的中点,
的中点,![]()
![]() 且
且![]()
同理:![]() ,
,![]()
![]()
在等腰Rt![]() 中,
中,![]()
![]()
![]()
![]()
![]()
![]()
![]() 同理:
同理:![]()
![]()
![]()
=![]()
![]() .
.
![]()
![]()
![]()
![]() 为等腰直角三角形.
为等腰直角三角形.
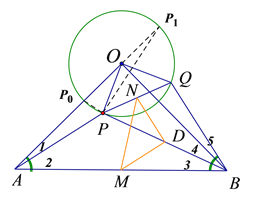
(3), 如图,设⊙![]() 交
交![]() 于点
于点![]() ,交
,交![]() 延长线于点
延长线于点![]() ,
,
连接![]()
![]() ,而
,而![]() ,
,
![]() 同理,
同理,![]()
由题意,![]() ,
,
![]()
![]() 的最小值为
的最小值为![]() . 同理,
. 同理,![]() 最大值为
最大值为![]() ,
,
从而得![]() 的最大值与最小值的差为:
的最大值与最小值的差为:![]()


科目:初中数学 来源: 题型:
【题目】某地区在一次九年级数学质量检测试题中,有一道分值为8分的解答题,所有考生的得分只有四种,即:0分,3分,5分,8分,老师为了解本题学生得分情况,从全区4500名考生试卷中随机抽取一部分,分析、整理本题学生得分情况并绘制了如下两幅不完整的统计图:
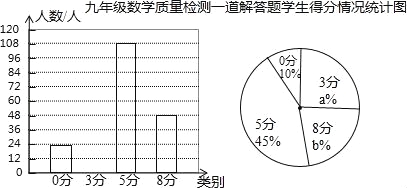
请根据以上信息解答下列问题:
(1)本次调查从全区抽取了 份学生试卷;扇形统计图中a= ,b= ;
(2)补全条形统计图;
(3)该地区这次九年级数学质量检测中,请估计全区考生这道8分解答题的平均得分是多少?得8分的有多少名考生?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】博物馆作为征集、典藏、陈列和研究代表自然和人类文化遗产实物的场所,其存在的目的是为公众提供知识、教育及欣赏服务.近年来,人们到博物馆学习参观的热情越来越高.2012-2018年我国博物馆参观人数统计如下:
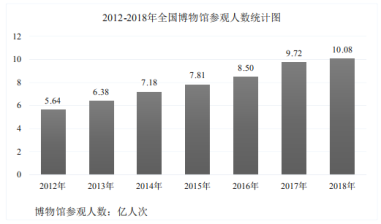
小明研究了这个统计图,得出四个结论:①2012年到2018年,我国博物馆参观人数持续增长;②2019年末我国博物馆参观人数估计将达到10.82亿人次;③2012年到2018年,我国博物馆参观人数年增幅最大的是2017年;④2016年到2018年,我国博物馆参观人数平均年增长率超过10%.其中正确的是( )
A.①③B.①②③C.①②④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为缓解扬州城区交通压力,城市南部快速通道已于4.18开工建设.某工程队承担了某道路900米长的改造任务.工程队在改造完360米道路后,引进了新设备,每天的工作效率比原来提高了20%,结果共用27天完成了任务,问引进新设备前工程队每天改造道路多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标都在格点上,且△A1B1C1与△ABC关于原点O成中心对称,C点坐标为(-2,1)。
(1)请直接写出A1的坐标 ;并画出△A1B1C1.
(2)P(a,b)是△ABC的AC边上一点,将△ABC平移后点P的对称点P'(a+2,b﹣6),请画出平移后的△A2B2C2.
(3)若△A1B1C1和△A2B2C2关于某一点成中心对称,则对称中心的坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果三角形三边的长a、b、c满足![]() ,那么我们就把这样的三角形叫做“匀称三角形”,如:三边长分别为1,1,1或3,5,7,…的三角形都是“匀称三角形”.
,那么我们就把这样的三角形叫做“匀称三角形”,如:三边长分别为1,1,1或3,5,7,…的三角形都是“匀称三角形”.
(1)如图1,已知两条线段的长分别为a、c(a<c).用直尺和圆规作一个最短边、最长边的长分别为a、c的“匀称三角形”(不写作法,保留作图痕迹);
(2)如图2,△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作⊙O的切线交AB延长线于点E,交AC于点F,若![]() ,判断△AEF是否为“匀称三角形”?请说明理由.
,判断△AEF是否为“匀称三角形”?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,规定把一个点先绕原点逆时针旋转45°,再作出它关于原点的对称点称为一次变换,已知点A的坐标为(﹣2,0),把点A经过连续2014次这样的变换得到的点A2014的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形![]() 是菱形,
是菱形,![]() ,反比例函数
,反比例函数![]() 的图象经过点
的图象经过点![]() ,若将菱形向下平移2个单位,点
,若将菱形向下平移2个单位,点![]() 恰好落在反比例函数的图象上,则反比例函数的表达式为( )
恰好落在反比例函数的图象上,则反比例函数的表达式为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com