
 如图,△ABC中,∠A=α,BI、CI分别平分∠ABC,∠ACB,则∠BIC=90°+$\frac{α}{2}$,若BM、CM分别为∠ABC,∠ACB的外角平分线,则∠M=90°-$\frac{α}{2}$.
如图,△ABC中,∠A=α,BI、CI分别平分∠ABC,∠ACB,则∠BIC=90°+$\frac{α}{2}$,若BM、CM分别为∠ABC,∠ACB的外角平分线,则∠M=90°-$\frac{α}{2}$. 分析 由∠A=α,三角形内角和等于180°,可得∠ABC+∠ACB=180°-α,又因为BI、CI分别平分∠ABC,∠ACB,所以∠IBC+∠ICB=$\frac{1}{2}(180°-α)$=90°$-\frac{α}{2}$,又因为∠IBC+∠ICB+∠BIC=180°,从而可以求得∠BIC的值;由BI、CI分别平分∠ABC,∠ACB,BM、CM分别为∠ABC,∠ACB的外角平分线,可得∠IBM=∠IBC=90°,则∠BIC+∠M=180°,从而求得∠M的值.
解答 解:∵∠A=α,∠A+∠ABC+∠ACB=180°,
∴∠ABC+∠ACB=180°-α.
∵BI、CI分别平分∠ABC,∠ACB,
∴∠IBC+∠ICB=$\frac{1}{2}(180°-α)$=90°$-\frac{α}{2}$.
∵∠IBC+∠ICB+∠BIC=180°,
∴∠BIC=90°+$\frac{α}{2}$.
∵BI、CI分别平分∠ABC,∠ACB,BM、CM分别为∠ABC,∠ACB的外角平分线,
∴∠IBM=∠IBC=90°.
∴∠BIC+∠M=180°.
∵∠BIC=90°+$\frac{α}{2}$,
∴∠M=90°-$\frac{α}{2}$.
故答案为:90°+$\frac{α}{2}$,90°-$\frac{α}{2}$.
点评 本题考查了三角形的内角和、角平分线的性质、三角形的外角的性质,关键是运用知识灵活变化,进而求出问题的答案.


科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
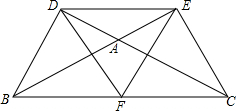 如图,在△ABC中,∠BAC>90°,DC⊥DB,BE⊥EC,F为BC上的一个动点,猜想:当F为于BC上的什么位置时,△FDE是等腰三角形,并证明你的猜想是正确的.
如图,在△ABC中,∠BAC>90°,DC⊥DB,BE⊥EC,F为BC上的一个动点,猜想:当F为于BC上的什么位置时,△FDE是等腰三角形,并证明你的猜想是正确的.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com