
【题目】如图,△ABC中,AB=AC,BE⊥AC于E,且D、E分别是AB、AC的中点.延长BC至点F,使CF=CE.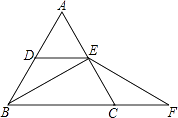
(1)求∠ABC的度数;
(2)求证:BE=FE;
(3)若AB=2,求△CEF的面积.
【答案】
(1)解:∵BE⊥AC于E,E是AC的中点,
∴△ABC是等腰三角形,即AB=BC,
∵AB=AC,
∴△ABC是等边三角形,
∴∠ABC=60°
(2)证明:∵CF=CE,
∴∠F=∠CEF,
∵∠ACB=60°=∠F+∠CEF,
∴∠F=30°,
∵△ABC是等边三角形,BE⊥AC,
∴∠EBC=30°,
∴∠F=∠EBC,
∴BE=EF
(3)解:过E点作EG⊥BC,如图:

∵BE⊥AC,∠EBC=30°,AB=BC=2,
∴BE= ![]() ,CE=1=CF,
,CE=1=CF,
在△BEC中,EG= ![]() ,
,
∴ ![]()
【解析】(1)根据等腰三角形的三线合一求出∠ABC的度数;(2)根据三角形的一个外角等于和它不相邻的两个内角的和、等腰三角形的性质得到BE=EF;(3)根据勾股定理求出BE的长,求出△CEF的面积.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
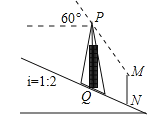
【题目】如图,信号塔PQ座落在坡度i=1:2的山坡上,其正前方直立着一警示牌.当太阳光线与水平线成60°角时,测得信号塔PQ落在斜坡上的影子QN长为![]() 米,落在警示牌上的影子MN长为3米,求信号塔PQ的高.(结果不取近似值)
米,落在警示牌上的影子MN长为3米,求信号塔PQ的高.(结果不取近似值)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A,B两地相距40千米,中午12:00时,甲从A地出发开车到B地,12:10时乙从B地出发骑自行车到A地,设甲行驶的时间为t(分),甲、乙两人离A地的距离S(千米)与时间t(分)之间的关系如图所示.由图中的信息可知,乙到达A地的时间为( )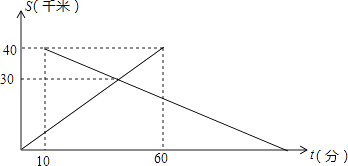
A.14:00 B.14:20 C.14:30 D.14:40
查看答案和解析>>
科目:初中数学 来源: 题型:
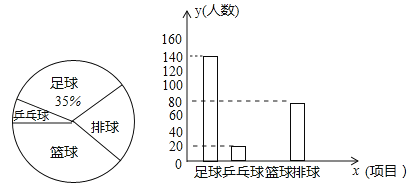
【题目】某校为提高学生身体素质,决定开展足球、篮球、台球、乒乓球四项课外体育活动,并要求学生必须并且只能选择一项.为了解选择各种体育活动项目的学生人数,随机抽取了部分学生进行调查,并绘制出以下两幅不完整的统计图.请根据统计图回答下列问题.(要求写出简要的解答过程)
(1)这次活动一共调查了多少名学生?
(2)补全条形统计图.
(3)若该学校总人数是1300人,请估计选择篮球项目的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式中从左到右的变形,是因式分解的是( )
A. (a+2)(a﹣2)=a2﹣4B. x2+x﹣1=(x﹣1)(x+2)+1
C. a+ax+ay=a(x+y)D. a2b﹣ab2=ab(a﹣b)
查看答案和解析>>
科目:初中数学 来源: 题型:
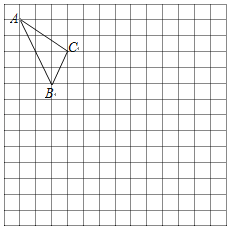
【题目】在如图的正方形网格中,每一个小正方形的边长为1.格点三角形ABC(顶点是网格线交点的三角形)的顶点A、C的坐标分别是(﹣4,6),(﹣1,4).
(1)请在图中的网格平面内建立平面直角坐标系;
(2)请画出△ABC关于x轴对称的△A1B1C1;
(3)请在y轴上求作一点P,使△PB1C的周长最小,并写出点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com