
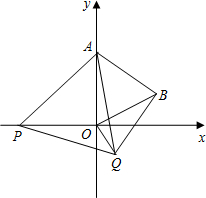
 ��ƽ��ֱ������ϵ����ͼ����֪��A��0��2������P��x����һ���㣬���߶�APΪһ�ߣ������Ҳ����ȱ�������APQ������P�˶���ԭ��O��ʱ����Q��λ��ΪB����֪��ֱ������������ֱ�DZߵ�ƽ���͵���б�ߵ�ƽ������ֱ����������ֱ�DZ߳�Ϊa��b��б�߳�Ϊc����a2+b2=c2��
��ƽ��ֱ������ϵ����ͼ����֪��A��0��2������P��x����һ���㣬���߶�APΪһ�ߣ������Ҳ����ȱ�������APQ������P�˶���ԭ��O��ʱ����Q��λ��ΪB����֪��ֱ������������ֱ�DZߵ�ƽ���͵���б�ߵ�ƽ������ֱ����������ֱ�DZ߳�Ϊa��b��б�߳�Ϊc����a2+b2=c2������ ��1����ͼ���������ߣ�֤����BOC=30�㣬OB=2������ֱ�������εı߽ǹ�ϵ���ɽ�����⣻
��2���������ۣ���Gλ��x���y�����������
��3��֤����APO�ա�AQB���õ���ABQ=��AOP=90�㣬���ɽ�����⣮
��� 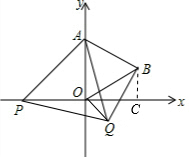 �⣺��1����ͼ������B��BC��x���ڵ�C��
�⣺��1����ͼ������B��BC��x���ڵ�C��
�ߡ�AOBΪ�ȱ������Σ���OA=2��
���AOB=60�㣬OB=OA=2��
���BOC=30�㣬����OCB=90�㣬
��BC=$\frac{1}{2}$OB=1��OC=$\sqrt{3}$��
���B������ΪB��$\sqrt{3}$��1����
��2������Gλ��x����ʱ����OG=OB����ʱG�������Ϊ����2��0����
��OB=BG����ʱ��G������Ϊ��2$\sqrt{3}$��0����
��OG=BG����ʱ��G������Ϊ��$\frac{2\sqrt{3}}{3}$��0����
����Gλ��y����ʱ����OG=OB����ʱG�������Ϊ��0����2����
��OB=BG����ʱ��G������Ϊ��0��2����
��OG=BG����ʱ��G������Ϊ��0��2����
�������������������ĵ�G������Ϊ������2��0����2$\sqrt{3}$��0����$\frac{2\sqrt{3}}{3}$��0����0����2����
��3����ABQ=90�㣬ʼ�ղ��䣮�������£�
�ߡ�APQ����AOB��Ϊ�ȱ������Σ�
��AP=AQ��AO=AB����PAQ=��OAB��
���PAO=��QAB��
�ڡ�APO���AQB�У�
$\left\{\begin{array}{l}{AP=AQ}\\{��PAO=��QAB}\\{AO=AB}\end{array}\right.$��
���APO�ա�AQB��SAS����
���ABQ=��AOP=90�㣮
���� �����ۺϿ����˵ȱ������ε����ʣ�ȫ�������ε��ж������ʣ����������ε��ж������ʣ�ע�����÷������۵ó��ǽ���ؼ���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
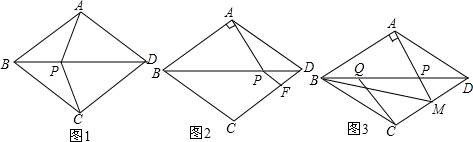 ��ͼ����ABD�ǵ��������Σ�AB=AD������ABD��BD���۵á�CBD����P���߶�BD��һ�㣬
��ͼ����ABD�ǵ��������Σ�AB=AD������ABD��BD���۵á�CBD����P���߶�BD��һ�㣬�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
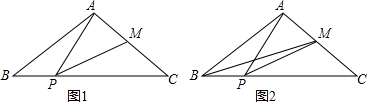 ��ͼ���ڡ�ABC�У���֪AB=AC=10��BC=16����p���߶�BC���˶���P����B��C�غϣ�������AP������APM=��B��PM��AC�ڵ�M��
��ͼ���ڡ�ABC�У���֪AB=AC=10��BC=16����p���߶�BC���˶���P����B��C�غϣ�������AP������APM=��B��PM��AC�ڵ�M���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{BC}{AB}$ | B�� | $\frac{AC}{AB}$ | C�� | $\frac{BC}{AC}$ | D�� | $\frac{AB}{BC}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
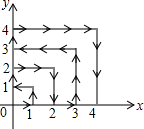 ��ͼ��һֻ�����ڵ�һ����x�ᡢy�����������ڵ�һ���ӣ�����ԭ����������1��0����Ȼ����Ű�ͼ�м�ͷ��ʾ��������������0��0������0��1������1��1������0��1����������ÿ������һ����λ����ô��35��ʱ��������λ�õ������ǣ�0��5����
��ͼ��һֻ�����ڵ�һ����x�ᡢy�����������ڵ�һ���ӣ�����ԭ����������1��0����Ȼ����Ű�ͼ�м�ͷ��ʾ��������������0��0������0��1������1��1������0��1����������ÿ������һ����λ����ô��35��ʱ��������λ�õ������ǣ�0��5�����鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com