
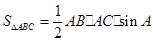 ;(2)根据题(1)得到的信息,请完成下题:如图2,在等腰△ABC中,AB=AC=12厘米,点P从A点出发,沿着边AB移动,点Q从C点出发沿着边CA移动,点Q的速度是1厘米/秒,点P的速度是点Q速度的2倍,若它们同时出发,设移动时间为t秒,问:当t为何值时,
;(2)根据题(1)得到的信息,请完成下题:如图2,在等腰△ABC中,AB=AC=12厘米,点P从A点出发,沿着边AB移动,点Q从C点出发沿着边CA移动,点Q的速度是1厘米/秒,点P的速度是点Q速度的2倍,若它们同时出发,设移动时间为t秒,问:当t为何值时,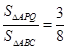 ?
? 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

 ; (B)
; (B) ; (C)
; (C) ; (D)60米。
; (D)60米。查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.扩大2倍; | B.缩小2倍; | C.扩大4倍; | D.大小不变 . |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com