
����Ŀ����ͼ1��������y��a��x+2����x��6����a��0����x�ύ��C��D���㣨��C�ڵ�D����ߣ�����y�Ḻ���ύ�ڵ�A��
��ͼ1��������y��a��x+2����x��6����a��0����x�ύ��C��D���㣨��C�ڵ�D����ߣ�����y�Ḻ���ύ�ڵ�A��
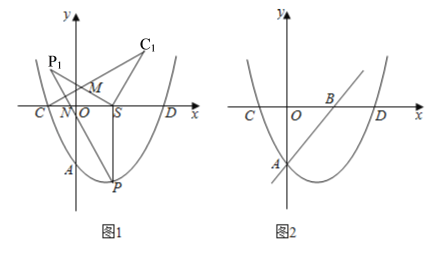
��1������ACD�����Ϊ16��
���������߽���ʽ��
��SΪ�߶�OD��һ�㣬��S��x��Ĵ��ߣ����������ڵ�P�����߶�SC��SP�Ƶ�S˳ʱ����ת������ͬ�Ľǵ�SC1��SP1��λ�ã�ʹ��C��P�Ķ�Ӧ��C1��P1����x���Ϸ���C1C��P1S���ڵ�M��P1P��x�ύ�ڵ�N����![]() �����ֵ��
�����ֵ��
��2����ͼ2��ֱ��y��x��12a��x�ύ�ڵ�B����M���������ϣ��������MAB��75��ĵ�M����ֻ����������a��ȡֵ��Χ��
��1������ACD�����Ϊ16��
���������߽���ʽ��
��SΪ�߶�OD��һ�㣬��S��x��Ĵ��ߣ����������ڵ�P�����߶�SC��SP�Ƶ�S˳ʱ����ת������ͬ�Ľǵ�SC1��SP1��λ�ã�ʹ��C��P�Ķ�Ӧ��C1��P1����x���Ϸ���C1C��P1S���ڵ�M��P1P��x�ύ�ڵ�N����![]() �����ֵ��
�����ֵ��
��2����ͼ2��ֱ��y��x��12a��x�ύ�ڵ�B����M���������ϣ��������MAB��75��ĵ�M����ֻ����������a��ȡֵ��Χ��
���𰸡���1����![]() ����
����![]() ���ֵΪ2����2��a��ȡֵ��ΧΪ
���ֵΪ2����2��a��ȡֵ��ΧΪ![]() ��
��
��������
��1�����������A��C��D�����꣬�Ӷ���CD��8��OA��12a�����S��ACD��16��������⣻�ڸ�����ת�������Լ�SAS��֤��P SP1C SC1������֤����MSC�ס�NSP1����![]() ����S(t��0)��0��t��6�����ɵ�
����S(t��0)��0��t��6�����ɵ�![]() ������������⣻
������������⣻
��2��������������ۣ��ٵ���M��y������ʱ����ʱ��MAO��30�㣬���ֱ��AM�Ľ���ʽ��![]() �������ɵõ�M�ĺ����꣬�г�����a�IJ���ʽ��������⣬�ڵ���M��y����Ҳ�ʱ�������Ƶķ����������M�ĺ����꣬�г�����a�IJ���ʽ��������⣮
�������ɵõ�M�ĺ����꣬�г�����a�IJ���ʽ��������⣬�ڵ���M��y����Ҳ�ʱ�������Ƶķ����������M�ĺ����꣬�г�����a�IJ���ʽ��������⣮
��1���������⣬��y��0����ã�x1����2��x2��6��
��C(��2��0)��D(6��0)��
��CD��8��
��x��0����ã�y����12a����a��0��
��A(0����12a)����OA��12a��
��S��ACD��![]() ��48a��16��
��48a��16��
��ã�![]() ��
��
�������ߵĽ���ʽΪ��![]() ��
��
�ڡ��߶�SC��SP�Ƶ�S˳ʱ����ת������ͬ�Ľǵ�SC1��SP1��λ�ã�
��SC= SC1��SP= SP1����P SP1=��C SC1��
��P SP1C SC1��SAS����
���SP1P=��SC1C����SCC1���ҡ�MSC����NSP1��
���MSC�ס�NSP1��
��![]() ��
��
��S(t��0)��0��t��6������SP1=SP��![]() ��SC��t+2��
��SC��t+2��
��![]() ��
��
��0��t��6��
�൱t��0ʱ��![]() ���ֵΪ2��
���ֵΪ2��
��2����ֱ��y��x��12a��x�ύ�ڵ�B��
��B(12a��0)��OA��OB��12a����OAB����OBA��45��,
�ٵ���M��y������ʱ����ʱ��MAO��30�㣬
��ֱ��AM��x�ύ�ڵ�E����OE��![]() ��
��
��E(![]() ��0)��
��0)��
�֡�A(0����12a)��
��ֱ��AM�Ľ���ʽΪ��![]() ��
��
����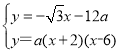 �� �ã�
�� �ã�![]() ��
��
��ã�![]() ����ȥ����
����ȥ����
���M�ĺ�����Ϊ��![]() ��
��
��![]() ��0��a��0��
��0��a��0��
��0��a��![]() ��
��
�ڵ���M��y����Ҳ�ʱ��������ֱ��AE����ֱ��AB�ĶԳ�ֱ�ߣ���ʱ��ֱ��AE�ĶԳ�ֱ���������ߵĽ��㣬��Ϊ��M������B��x��Ĵ�����ֱ��AE����AB�ĶԳ�ֱ�߽��ڵ�F�����EBA�ա�FBA��
���BAF����BAE =75�㣬BF��BE��![]() ����FBO��90�㣬
����FBO��90�㣬
��F(12a��![]() )��
)��
��ֱ��AF�Ľ���ʽΪ��![]() ��
��
����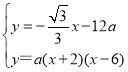 ����ã�
����ã�![]() ����ȥ����
����ȥ����
���M����������![]() ��
��
��![]() ��a��0��
��a��0��
��a��![]() ��
��
������������Ҫʹ�����MAB��75��ĵ�M����ֻ����������a��ȡֵ��ΧΪ��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
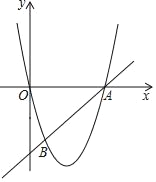
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�ֱ��AB��������y��ax2+bx���ڵ�A��6��0���͵�B��1����5����
��1�������������ߵı���ʽ��ֱ��AB�ı���ʽ��
��2�������C��ֱ��AB�ϣ��ҡ�BOC������ֵ��![]() �����C�����꣮
�����C�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ���꼶��������ѧ�������������������������������鲿��ѧ���ijɼ������ݳ�������Ƴ����µ�ͳ��ͼ��
��� | ����x | Ƶ�� |
A | 40��x��50 | 20 |
B | 50��x��60 | 30 |
C | 60��x��70 | 50 |
D | 70��x��80 | m |
E | 80��x��90 | 40 |
����������Ϣ����������⣺
��1���������������ѧ����ͳ��ͼ���У�m���������벹ȫֱ��ͼ��
��2��������ͳ��ͼ����B��������Ӧ��Բ�ĽǵĶ�����
��3�������꼶����800��ѧ��������������60��Ϊ�ϸ�������㱾�α���ȫ�꼶��
��ѧ��������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
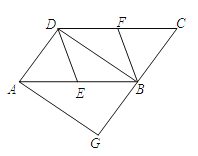
����Ŀ����֪����ͼ����![]() �У�
�У�![]() �ֱ��ڱ�
�ֱ��ڱ�![]() ���е㣬
���е㣬![]() �ǶԽ��ߣ�����
�ǶԽ��ߣ�����![]() ��
��![]() ����
����![]() ���ӳ�����
���ӳ�����![]() ��
��
��1����֤���ı���![]() ��ƽ���ı��Σ�
��ƽ���ı��Σ�
��2�����ı���![]() �Ǿ��Σ����ı���
�Ǿ��Σ����ı���![]() ��ʲô�����ı��Σ���֤����Ľ��ۣ�
��ʲô�����ı��Σ���֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
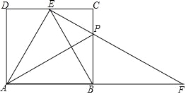
����Ŀ����ͼ���ھ���ABCD�У�AB=2��AD=![]() ���ڱ�CD����һ��E��ʹEBƽ�֡�AEC����PΪBC����һ�㣬��BP=2CP������EP���ӳ���AB���ӳ�����F����������������ۣ�
���ڱ�CD����һ��E��ʹEBƽ�֡�AEC����PΪBC����һ�㣬��BP=2CP������EP���ӳ���AB���ӳ�����F����������������ۣ�
�ٵ�Bƽ���߶�AF����PF=![]() DE���ۡ�BEF=��FEC����S����ABCD=4S��BPF���ݡ�AEB���������Σ�
DE���ۡ�BEF=��FEC����S����ABCD=4S��BPF���ݡ�AEB���������Σ�
������ȷ���۵�����ǣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڰ�ԲO�У�ABΪֱ����AC��ADΪ�����ң��ҡ�CAD+��CAB��90�㣮
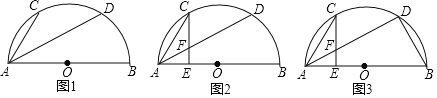
��1����ͼ1����֤����AC���ڻ�CD��
��2����ͼ2����E��ֱ��AB�ϣ�CE��AD�ڵ�F����AF��CF����֤��AD��2CE��
��3����ͼ3���ڣ�2���������£�����BD����AE��4��BD��12������AC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ����ʵ����ƶ��С���ĺ�ΰĿ�꣬���н�ϱ��طḻ��ɽˮ��Դ��������չ����ҵ������ׯ�ڵ���������֧���£��������������磬ר�ŽӴ��οͣ������繲��80��ͷ������ݺ������ṩ�ķ��䵥��x��Ԫ�����ο;�ס������y���䣩����Ϣ�����ֻ��Ƴ�y��x�ĺ���ͼ����ͼ��ʾ��
��1����y��x֮��ĺ�����ϵʽ��
��2��������涨ÿ������۸���60Ԫ�Ҳ�����150Ԫ�������ο�����ס��ÿ�����䣬������ÿ����֧��20Ԫ�ĸ��ַ��ã����۶�Ϊ����ʱ��������ÿ����������������Ƕ��٣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����Ϊ���˽�괺��ʱѧ���ĸ������������������һ��ѧУ�ij����꼶�������ȡ�˲���ѧ����������������е��飬�����ⲿ��ѧ�������Ѷ���Ƴ�Ƶ�ʷֲ�ֱ��ͼ����֪�������ҵ�һ�������Ϊ12�����������������Ϣ�ش�

��1������ȡ�����ѧ������Ϊ ����
��2���������ҵ������Ƶ���� ��
��3������ÿ���ƽ�����Ѷ��Ը������Сֵ���㣬��ô����ȡѧ�����ε����ƽ�����Ѷ�Ϊ Ԫ��
��4���Եڣ�3��С������õ����ƽ�����Ѷ������Ƹõ���ȫ��ѧ�����ε����ƽ�����Ѷ����Ϊ�Ƿ��������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
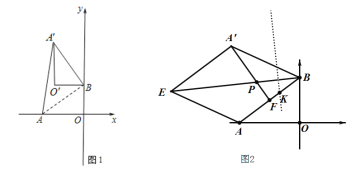
����Ŀ����ƽ��ֱ������ϵ�У�OΪԭ�㣬��A(4��0)����B(0��3)����ABO�Ƶ�B˳ʱ����ת������A��BO������A��O��ת��Ķ�Ӧ��ΪA����O��������ת��Ϊ����
(1)��ͼ1������=90������AA���ij���
(2)��(1)�������£���OA����һ��M��ת��Ķ�Ӧ��ΪN����O��M+BNȡ����Сֵʱ����ͼ�л������M��λ�ã��������N�����ꡣ
(3)��ͼ2������ABO�Ƶ�B˳ʱ����ת�����У���AB��A��BΪ�ڱ�����AB A��E��F��AB���е㣬��A��F��BE��P��BP�Ĵ�ֱƽ���߽�AB��K��������60����90���ı仯�����У���K��λ���Ƿ�仯�������䣬��BK�ij���ֱ��д���˱仯�����е�P���˶�·������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com