
【题目】如图,AB是⊙O的直径,C、D为半圆O上的两点,CD∥AB,过点C作CE⊥AD,交AD的延长线于点E,tanA=![]() .
.
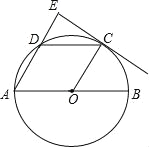
(1)求证:CE是⊙O的切线;
(2)猜想四边形AOCD是什么特殊的四边形,并证明你的猜想.
【答案】(1)证明见解析;(2)四边形AOCD是菱形;理由见解析.
【解析】
试题分析:(1)连接OD,由锐角三角函数得出∠A=60°,证出△OAD是等边三角形,得出∠ADO=∠AOD=60°,再证明△COD是等边三角形,得出∠COD=60°=∠ADO,证出OC∥AE,由已知条件得出CE⊥OC,即可得出结论;
(2)由(1)得:△OAD和△COD是等边三角形,得出OA=AD=OD=CD=OC,即可证出四边形AOCD是菱形.
试题解析:(1)连接OD,如图所示:
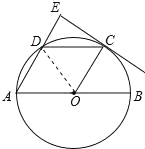
∵tanA=![]() ,
,
∴∠A=60°,
∵OA=OD,
∴△OAD是等边三角形,
∴∠ADO=∠AOD=60°,
∵CD∥AB,
∴∠ODC=60°,
∵OC=OD,
∴△COD是等边三角形,
∴∠COD=60°=∠ADO,
∴OC∥AE,
∵CE⊥AE,
∴CE⊥OC,
∴CE是⊙O的切线;
(2)四边形AOCD是菱形;理由如下:
由(1)得:△OAD和△COD是等边三角形,
∴OA=AD=OD=CD=OC,
∴四边形AOCD是菱形.


 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:
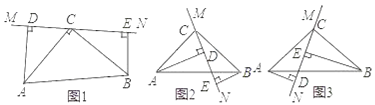
【题目】在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图1的位置时,求证:①△ADC≌△CEB;②DE=AD+BE;
(2)当直线MN绕点C旋转到图2的位置时,求证:DE=AD﹣BE;
(3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的有( ):①单项式必须是同类项才能相乘;②几个单项式的积,仍是单项式;③几个单项式之和仍是单项式;④几个单项式相乘,有一个因式为0,积一定为0.
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将二次函数y=x2的图象向下平移一个单位,则平移以后的二次函数的解析式为( )
A.y=x2-1 B.y=x2+1
C.y=(x-1)2 D.y=(x+1)2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC.
(1)用尺规作图的方法分别作出△ABC的角平分线BE和CF, 且BE和CF交于点O.(保留作图痕迹,不要求写出作法);
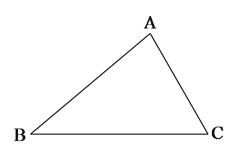
(2)在(1)中,如果∠ABC=40°,,∠ACB=60°,求∠BOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为鼓励居民节约用电,广州市自2012年以来对家庭用电收费实行阶梯电价,即每月对每户居民的用电量分为三个档级收费,第一档为用电量在180千瓦时(含180千瓦时)以内的部分,执行基本价格;第二档为用电量在180千瓦时到450千瓦时(含450千瓦时)的部分,实行提高电价;第三档为用电量超出450千瓦时的部分,比第二档的单价每千瓦时提高0.05元. 海珠区的李白同学家今年2月份用电330千瓦时,电费为213元,3月份用电240千瓦时,电费为150元.已知我市的另一位居民杜甫家今年4、5月份的家庭用电量分别为200和 490千瓦时,请你依据题目条件,计算杜甫家4、8月份的电费分别为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com