
 小明将一副三角板按如图所示摆放在一起,发现只要知道AB,BD,DC,CA四边中的其中一边的长就可以求出其他各边的长,若已知AB=2,则CD的长为________.
小明将一副三角板按如图所示摆放在一起,发现只要知道AB,BD,DC,CA四边中的其中一边的长就可以求出其他各边的长,若已知AB=2,则CD的长为________. 优生乐园系列答案
优生乐园系列答案科目:初中数学 来源: 题型:
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |

查看答案和解析>>
科目:初中数学 来源: 题型:
 小明将一副三角板按如图所示摆放在一起,发现只要知道AB,BD,DC,CA四边中的其中一边的长就可以求出其他各边的长,若已知AB=2,则CD的长为
小明将一副三角板按如图所示摆放在一起,发现只要知道AB,BD,DC,CA四边中的其中一边的长就可以求出其他各边的长,若已知AB=2,则CD的长为| 6 |
| 6 |
查看答案和解析>>
科目:初中数学 来源:2013年江苏省南京市联合体(栖霞下关雨花台等)九年级中考一模数学试卷(带解析) 题型:解答题
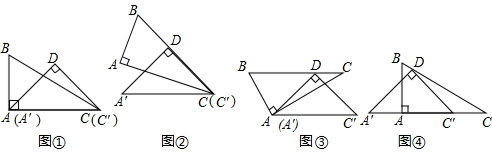
小明在玩一副三角板时发现:含45°角的直角三角板的斜边可与含30°角的直角三角板的较长直角边完全重合(如图①).即△C´DA´的顶点A´、C´分别与△BAC的顶点A、C重合.现在,他让△C´DA´固定不动,将△BAC通过变换使斜边BC经过△C´DA´的直角顶点D.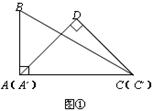
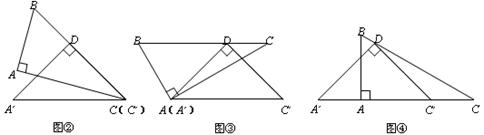
(1)如图②,将△BAC绕点C按顺时针方向旋转角度α(0°<α<180°),使BC边经过点D,则α= °.
(2)如图③,将△BAC绕点A按逆时针方向旋转,使BC边经过点D.试说明:BC∥A´C´.
(3)如图④,若AB=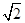 ,将将△BAC沿射线A´C´方向平移m个单位长度,使BC边经过点D,求m的值.
,将将△BAC沿射线A´C´方向平移m个单位长度,使BC边经过点D,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com