
 由四个相同的小正方形拼成如图,能否将连续的24个自然数分别放在图中所示的24个黑点处(每处放一个,每个数只使用一次)使得图中所有正方形边上所放的数之和都相等?若能,请给出一个例子;若不能,请说明理由.
由四个相同的小正方形拼成如图,能否将连续的24个自然数分别放在图中所示的24个黑点处(每处放一个,每个数只使用一次)使得图中所有正方形边上所放的数之和都相等?若能,请给出一个例子;若不能,请说明理由. 分析 不能,设放的最小的自然数为a,则放的最大的自然数为a+23,得到这24个自然数的和为A=12(2a+23).假设可能,设每个正方形边上所放的数之和为S,因为共有5个正方形,这些和的和为5S,因为每个数在这些和中出现两次,所以5S=2A,记最小的16个数的和为B,则B=8(2a+15),再分两种情况讨论:(1)B≤S;(2)B>S即可求解.
解答 解:不能,
设放的最小的自然数为a,则放的最大的自然数为a+23,
那么,这24个自然数的和为A=24a+276=12(2a+23).
假设可能,每个正方形边上的数之和为S,
因为共有5个正方形,所以这些正方形的数字的和为5S,
我们发现每个数在这些和中出现两次,所以5S=2A,
记最小的16个数的和为B,则B=8(2a+15),
①B≤S,则S=$\frac{2}{5}$A=$\frac{24}{5}$(12a+23)≥8(2a+15),即9.8a+110.4≥16a+120,
不存在自然数a使不等式成立;
②B>S,因为此时不可能选择最大正方形边上的16个数字使16个数的和等于S,
所以,也不可能.
点评 本题考查了作图-应用与设计作图以及数字和的问题,运用了整体思想和分类思想,有一定的难度.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
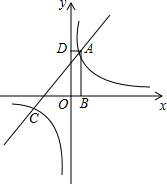 如图,矩形ABCD的顶点A是函数y=$\frac{k}{x}$的图象与函数y=x+(k-1)的图象在第一象限的交点,两函数图象另一交点为点C,AB垂直于x轴,垂足为点B,AD垂直于y轴,垂足为点D,且矩形ABOD的面积为5.
如图,矩形ABCD的顶点A是函数y=$\frac{k}{x}$的图象与函数y=x+(k-1)的图象在第一象限的交点,两函数图象另一交点为点C,AB垂直于x轴,垂足为点B,AD垂直于y轴,垂足为点D,且矩形ABOD的面积为5.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 第一次向右拐50°第二次向左拐130° | |
| B. | 第一次向左拐30°第二次向右拐30° | |
| C. | 第一次向右拐50°第二次向右拐130° | |
| D. | 第一次向左拐50°第二次向左拐130° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com