
如图,在平面直角坐标系中,直线y=x+4与x轴、y轴分别交于A、B两点,抛物线y=﹣x2+bx+c经过A、B两点,并与x轴交于另一点C(点C点A的右侧),点P是第二象限的抛物线上一动点.

(1)求抛物线的解析式及点C的坐标;
(2)当点P运动到什么位置时,△PAB的面积最大?最大面积是多少?
(3)当(2)中点P运动到△PAB的面积最大时,x轴上是否存在点D,使△PDB的周长最小,若存在,求出点D的坐标,若不存在。请说明理由。
(1)抛物线解析式为y=-x2-3x+4.C(1,0).(2)P(-2,6),8;(3)点D的坐标为(- ,0).
,0).
【解析】
试题分析:(1)把A(-4,0),B(0,4)代入抛物线y=-x2+bx+c,可得出抛物线解析式,当y=0时即可得出点C的坐标.
(2)设y=x+b与抛物线y=-x2-3x+4只有一个交点时,△PAB的面积最大,利用判别式求出b的值,再联立可得出点P的坐标,过点B作BM⊥PN交PN于点M,利用三角函数求出BM,再利用△PAB的面积公式即可求出答案.
(3)连接BP,作点B关于原点O的对称点B′,连接B′P,交x轴于点D,这时△PDB的周长最小.先求出点B′的坐标,再利用坐标求出PB′所在的直线,即可求出与x轴的交点D的坐标.
试题解析:(1)∵直线y=x+4与x轴、y轴分别交于A、B两点,
∴A(-4,0),B(0,4)抛物线y=-x2+bx+c经过A、B两点,可得
 ,
,
解得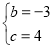 ,
,
∴抛物线解析式为y=-x2-3x+4.
令y=0,得-x2-3x+4=0,
解得x1=-4,x2=1,
∴C(1,0).
(2)如图1,
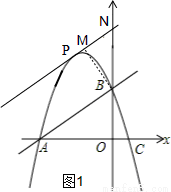
设y=x+b与抛物线y=-x2-3x+4只有一个交点时,△PAB的面积最大,
∵由x+b=-x2-3x+4化简x2+4x+b-4只有一个解,得△=16-4×(b-4)=32-4b=0,解得b=8.
∴y=x+8,
∴联立得方程组得 ,
,
解得 ,
,
∴P(-2,6)
过点B作BM⊥PN交PN于点M,
∵BN=ON-OB=8-4=4,sin∠MNB= ,
,
∴BM=4× =2
=2 ,
,
△PAB的面积= ABBM=
ABBM= ×4
×4 ×2
×2 =8.
=8.
(3)存在.
如图2,

连接BP,作点B关于原点O的对称点B′,连接B′P,交x轴于点D,这时△PDB的周长最小.
∵点B(0,4),
∴点B′(0,-4),
∵P(-2,6)
∴设PB′所在的直线为y=kx+b得
 ,
,
解得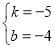
∴PB′所在的直线为y=-5x-4,
点D的坐标为(- ,0).
,0).
考点:二次函数综合题.


科目:初中数学 来源:2014-2015学年云南省腾冲县六校九年级上学期期末联考数学试卷(解析版) 题型:选择题
方程 的两根分别是⊙
的两根分别是⊙ 和⊙
和⊙ 的半径,且两圆相切,则圆心距
的半径,且两圆相切,则圆心距 为( ).
为( ).
A、 1 B、9 C、4或5 D、1或9
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省简阳市镇金学区九年级上学期12月月考数学试卷(解析版) 题型:填空题
用一条长为30cm的铁丝围成一个斜边长为13cm的直角三角形,则这个直角三角形的面积为_______ cm 2 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省简阳市镇金学区九年级上学期12月月考数学试卷(解析版) 题型:选择题
太阳光照射下的某一时刻,1.5m高的竹竿影长2.5m,那么影长为30m的旗杆的高是( ).
A 、20m B、18m C、16m D、15m
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省九年级上学期期中考试数学试卷(解析版) 题型:解答题
某学校为了改善办学条件,计划购置一批电子白板和一批笔记本电脑,经投标,购买1块电子白板比买3台笔记本电脑多3000元,购买4块电子白板和5台笔记本电脑共需80000元.
(1)求购买1块电子白板和一台笔记本电脑各需多少元?
(2)根据该校实际情况,需购买电子白板和笔记本电脑的总数为396,要求购买的总费用不超过2700000元,并购买笔记本电脑的台数不超过购买电子白板数量的3倍,该校有哪几种购买方案?
(3)上面的哪种购买方 案最省钱?按最省钱方案购买需要多少钱?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东潍坊高密四中文慧学校九年级上学期第一次月考数学试卷(解析版) 题型:解答题
如图,在Rt△ACB中,∠C=90°,CD⊥AB,垂足为点D.

(1)写出图中的三对相似三角形,并选择其中一对进行证明;
(2)如果AC=6,BC=8,求AD的长.
查看答案和解析>>
科目:初中数学 来源:2015年上海市四区联考九年级一模数学试卷(解析版) 题型:选择题
如图,已知在梯形 中,
中, ∥
∥ ,
, ,如果对角线
,如果对角线 与
与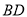 相交于点
相交于点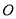 ,
,
△ 、△
、△ 、△
、△ 、△
、△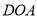 的面积分别记作
的面积分别记作 、
、 、
、 、
、 ,那么下列结论中,不正确的
,那么下列结论中,不正确的
是( )

A.  ; B.
; B.  ; C.
; C. 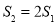 ; D.
; D.  ;
;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com