
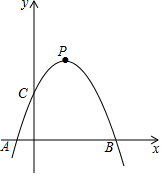
 ШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌХзЮяЯпy=-$\frac{1}{2}$x2+bx+cгыxжсНЛгкЕуAЁЂBЃЌЕуAЕФКсзјБъЮЊ-1ЃЎгыyжсНЛгкЕуCЃЌЕуCЕФзнзјБъЮЊ2ЃЎЖЅЕуЮЊPЃЎЙ§ЖЏЕуH ЃЈ0ЃЌmЃЉзїЦНаагкxжсЕФжБЯпlЃЌжБЯпlгыХзЮяЯпЯрНЛгкЕуDЁЂEЃЎ
ШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌХзЮяЯпy=-$\frac{1}{2}$x2+bx+cгыxжсНЛгкЕуAЁЂBЃЌЕуAЕФКсзјБъЮЊ-1ЃЎгыyжсНЛгкЕуCЃЌЕуCЕФзнзјБъЮЊ2ЃЎЖЅЕуЮЊPЃЎЙ§ЖЏЕуH ЃЈ0ЃЌmЃЉзїЦНаагкxжсЕФжБЯпlЃЌжБЯпlгыХзЮяЯпЯрНЛгкЕуDЁЂEЃЎЗжЮі ЃЈ1ЃЉгУД§ЖЈЯЕЪ§ЗЈжБНгЧѓГіХзЮяЯпНтЮіЪНЃЌдйХфГЩЖЅЕуЪНЃЌШЗЖЈГіЖЅЕузјБъЃЛ
ЃЈ2ЃЉЯШИљОнИљгыЯЕЪ§ЕФЙиЯЕЃЌгЩЁбQгыxжсЯрЧаЃЌШЗЖЈГіmЕФжЕЃЌдйШЗЖЈГіЕуPЙигкжБЯпlЕФЖдГЦЕуP1ЕФзјБъЃЌНјЖјНтГіНсТлЃЛ
ЃЈ3ЃЉЗжжБНЧЖЅЕуЪЧAЃЌCЃЌPШ§жжЧщПігУЦНУцзјБъЯЕФкЃЌСНЕуМфЕФОрРыЙЋЪНБэЪОГіЯпЖЮЃЌШЛКѓНЈСЂЗНГЬЧѓНтМДПЩЃЎ
НтД№ НтЃКЃЈ1ЃЉгЩЬтвтЃКАбAЕузјБъЃЈ-1ЃЌ0ЃЉЃЌCЕузјБъЃЈ0ЃЌ2ЃЉДњШыy=-$\frac{1}{2}$x2+bx+cжаНтЕУЃК
Ёрb=$\frac{3}{2}$ЃЌc=2ЃЎ
Ёрy=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2=-$\frac{1}{2}$ЃЈx-$\frac{3}{2}$ЃЉ2+$\frac{25}{8}$
ЁрЖЅЕуPЕФзјБъЃКЃЈ$\frac{3}{2}$ЃЌ$\frac{25}{8}$ЃЉЃЌ
ЃЈ2ЃЉШчЭМ1ЃЌ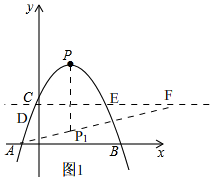
Сюy=mЃЌ-$\frac{1}{2}$x2+$\frac{3}{2}$x+2=mЃЌ
ЩшDЃЈx1ЃЌ0ЃЉЃЌEЃЈx2ЃЌ0ЃЉЃЌ
Ёрx1ЁЂx2ЪЧИУЗНГЬЕФСНИіИљЃЌдђx2-3x-4+2m=0ЃЌ
Ыљвдx1+x2=3ЃЌx1x2=-4+2mЃЌ
ЁрDE2=|x1-x2|2=ЃЈx1+x2ЃЉ2-4x1x2=9-ЃЈ-4+2mЃЉ=25-8mЃЎ
ЁпвдDEЮЊжБОЖЕФЁбOгыxжсЯрЧаЃЌ
ЁрDE=2mЃЌМД25-8m=4m2ЃЌНтЕУm=-1ЁР$\frac{\sqrt{29}}{2}$ЃЎ
ЁпmЃО0ЃЌ
Ёрm=-1+$\frac{\sqrt{29}}{2}$ЃЎ
ЁпДЫЪБдкжБЯпlЩЯДцдквЛЕуFЃЌТњзу|PF-AF|газюДѓжЕЃЎ
СюЖЅЕуPЙигкжБЯпlЕФЖдГЦЕуЮЊP1ЃЌПЩЧѓЕУP1зјБъЮЊЃЈ$\frac{3}{2}$ЃЌ$\sqrt{29}-\frac{41}{8}$ЃЉ
ИљОнжсЖдГЦаджЪЕУЃКPF=P1FЃЌ
Ёр|PF-AF|=|P1F-AF|ЃЎ
взЕУAЁЂP1ЁЂFдкЭЌвЛЬѕжБЯпЩЯЪБЃЌ|P1F-AF|жЕзюДѓЮЊA P1ЃЎ
ЁржБЯпAFЕФКЏЪ§БэДяЪНКЭжБЯпA P1ЯрЭЌЃЌЩшЮЊy1=kx+n
ДњШыAЕузјБъЃЈ-1ЃЌ0ЃЉЕУЃЌP1ЕузјБъЃЈ$\frac{3}{2}$ЃЌ$\sqrt{29}-\frac{41}{8}$ЃЉ
ЕУk=n=$\frac{2}{5}\sqrt{29}-\frac{41}{20}$
ЁржБЯпAFЕФКЏЪ§БэДяЪНy1=ЃЈ$\frac{2}{5}\sqrt{29}-\frac{41}{20}$ЃЉЃЈx+1ЃЉ
y1=ЃЈ$\frac{2}{5}\sqrt{29}-\frac{41}{20}$ЃЉx+$\frac{2}{5}\sqrt{29}-\frac{41}{20}$
ЃЈ3ЃЉЂйвдЕуCЮЊжБНЧЖЅЕуЪБЃЌ
ЁпAЕузјБъЃЈ-1ЃЌ0ЃЉЃЌCЕузјБъЃЈ0ЃЌ2ЃЉЃЎ
ЁржБЯпACНтЮіЪНЮЊy=2x+2ЃЌAC=$\sqrt{5}$
ЁржБЯпCPНтЮіЪНЮЊy=-$\frac{1}{2}$x+2ЃЌ
ЁпЕуPдкжБЯпy=mЩЯЃЎ
ЁрЕуPЕФзјБъЮЊЃЈ4-2mЃЌmЃЉЃЌ
ЁрCP=$\sqrt{ЃЈ4-2mЃЉ^{2}+ЃЈm-2ЃЉ^{2}}$
ЁпЁїACGЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁрAC=CPЃЌ
Ёр$\sqrt{5}$=$\sqrt{ЃЈ4-2mЃЉ^{2}+ЃЈm-2ЃЉ^{2}}$
Ёрm=1Лђm=3
ЂквдЕуAЮЊжБНЧЖЅЕуЪБЃЌ
жБЯпAPНтЮіЪНЮЊy=-$\frac{1}{2}$x-$\frac{1}{2}$ЃЌ
ЩшPЃЈ-2m-1ЃЌmЃЉЃЌ
ЁрAP=$\sqrt{ЃЈ-2m-1+1ЃЉ^{2}+{m}^{2}}$ЃЌ
ЁпЁїACGЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁрAC=APЃЌ
Ёр$\sqrt{5}$=$\sqrt{ЃЈ-2m-1+1ЃЉ^{2}+{m}^{2}}$ЃЌ
Ёрm=ЁР1ЃЌ
ЂлвдЕуPЮЊжБНЧЖЅЕуЪБЃЌЩшPЃЈnЃЌmЃЉЃЌ
ЁрPA=$\sqrt{ЃЈn+1ЃЉ^{2}+{m}^{2}}$ЃЌPC=$\sqrt{{n}^{2}+ЃЈm-2ЃЉ^{2}}$
ЁпAЃЈ-1ЃЌ0ЃЉЃЌCЃЈ0ЃЌ2ЃЉЃЌ
ЁрACЕФжаЕуMЃЈ-$\frac{1}{2}$ЃЌ1ЃЉЃЌ
ЁрPM=$\sqrt{ЃЈn+\frac{1}{2}ЃЉ^{2}+ЃЈm-1ЃЉ^{2}}$ЃЌ
ЁпЁїACGЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁрPM=$\frac{1}{2}$ACЃЌPA=PCЃЌ
Ёр$\frac{\sqrt{5}}{2}$=$\sqrt{ЃЈn+\frac{1}{2}ЃЉ^{2}+ЃЈm-1ЃЉ^{2}}$ЂйЃЌ
$\sqrt{ЃЈn+1ЃЉ^{2}+{m}^{2}}$=$\sqrt{{n}^{2}+ЃЈm-2ЃЉ^{2}}$ЂкЃЌ
СЊСЂЂйЂкНтЕУЃЌm=$\frac{1}{2}$Лђm=$\frac{3}{2}$
злЩЯЫљЪіЃЌmЕФжЕЮЊ-1ЁЂ$\frac{1}{2}$ЁЂ1ЁЂ$\frac{3}{2}$ЁЂ3ЃЎ
ЕуЦР ДЫЬтЪЧЖўДЮКЏЪ§злКЯЬтЃЌжївЊПМВщД§ЖЈЯЕЪ§ЗЈЃЌМЋжЕЃЌЖдГЦЕФаджЪЃЌЕШбќжБНЧШ§НЧаЮЕФаджЪЃЌвЛдЊЖўДЮЗНГЬЕФИљгыЯЕЪ§ЕФЙиЯЕЃЌНтБОЬтЕФЙиМќЪЧгУЗНГЬЕФЫМЯыНтОіЮЪЬтЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
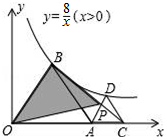 ШчЭМЃЌЁїAOBКЭЁїACDОљЮЊе§Ш§НЧаЮЃЌЖЅЕуBЁЂDдкЫЋЧњЯпy=$\frac{8}{x}$ЃЈxЃО0ЃЉЩЯЃЌЯпЖЮBCЁЂADНЛгкЕуPЃЌдђSЁїOBP=8ЃЎ
ШчЭМЃЌЁїAOBКЭЁїACDОљЮЊе§Ш§НЧаЮЃЌЖЅЕуBЁЂDдкЫЋЧњЯпy=$\frac{8}{x}$ЃЈxЃО0ЃЉЩЯЃЌЯпЖЮBCЁЂADНЛгкЕуPЃЌдђSЁїOBP=8ЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
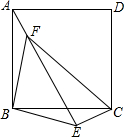 ЕуEдке§ЗНаЮABCDЭтЃЌBE=4ЃЌCE=2ЃЌЁЯBEC=135ЁуЃЌНЋЁїBECШЦЕуBФцЪБеыа§зЊЕУЕНЁїBFAЃЌЧѓFEЁЂFCЕФГЄЃЎ
ЕуEдке§ЗНаЮABCDЭтЃЌBE=4ЃЌCE=2ЃЌЁЯBEC=135ЁуЃЌНЋЁїBECШЦЕуBФцЪБеыа§зЊЕУЕНЁїBFAЃЌЧѓFEЁЂFCЕФГЄЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
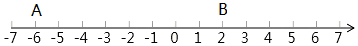
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
 ШчЭМЫљЪОЃЌгУДњЪ§ЪНБэЪОЭМжавѕгАВПЗжЕФУцЛ§ЃЌВЂМЦЫуx=6ЪБЃЌвѕгАВПЗжЕФУцЛ§ЃЎЃЈІаШЁ3.14ЃЉ
ШчЭМЫљЪОЃЌгУДњЪ§ЪНБэЪОЭМжавѕгАВПЗжЕФУцЛ§ЃЌВЂМЦЫуx=6ЪБЃЌвѕгАВПЗжЕФУцЛ§ЃЎЃЈІаШЁ3.14ЃЉВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com