
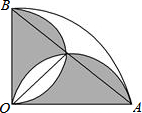
 半径1cm,圆心角90度的扇形OAB中,分别以OA,OB为直径作半圆,则阴影部分(两个半圆除了重叠部分其余部分)面积为$\frac{1}{2}$.
半径1cm,圆心角90度的扇形OAB中,分别以OA,OB为直径作半圆,则阴影部分(两个半圆除了重叠部分其余部分)面积为$\frac{1}{2}$. 分析 过点C作CD⊥OB,CE⊥OA,则△AOB是等腰直角三角形,由∠ACO=90°,可知△AOC是等腰直角三角形,由HL定理可知Rt△OCE≌Rt△ACE,故可得出S扇形OEC=S扇形AEC$\widehat{OC}$与弦OC围成的弓形的面积等于$\widehat{AC}$与弦AC所围成的弓形面积,S阴影=S△AOB即可得出结论.
解答 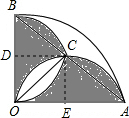 解:过点C作CD⊥OB,CE⊥OA,
解:过点C作CD⊥OB,CE⊥OA,
∵OB=OA,∠AOB=90°,
∴△AOB是等腰直角三角形,
∵OA是直径,
∴∠ACO=90°,
∴△AOC是等腰直角三角形,
∵CE⊥OA,
∴OE=AE,OC=AC,
在Rt△OCE与Rt△ACE中,
∵$\left\{\begin{array}{l}{OC=AC}\\{OE=AE}\end{array}\right.$,
∴Rt△OCE≌Rt△ACE,
∵S扇形OEC=S扇形AEC,
∴$\widehat{OC}$与弦OC围成的弓形的面积等于$\widehat{AC}$与弦AC所围成的弓形面积,
同理可得,$\widehat{OC}$与弦OC围成的弓形的面积等于$\widehat{BC}$与弦BC所围成的弓形面积,
∴S阴影=S△AOB=$\frac{1}{2}$×1×1=$\frac{1}{2}$cm2.
故答案为:$\frac{1}{2}$.
点评 本题考查的是扇形面积的计算与等腰直角三角形的判定与性质,根据题意作出辅助线,构造出直角三角形得出S阴影=S△AOB是解答此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
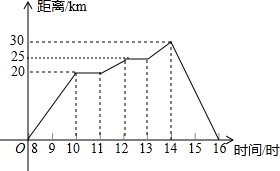 假日里,小亮和爸爸骑自行车郊游,上午8时从家出发,16时返回家中,他们离家的距离与时间的关系可用图中的折线表示.
假日里,小亮和爸爸骑自行车郊游,上午8时从家出发,16时返回家中,他们离家的距离与时间的关系可用图中的折线表示.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com