
【题目】如图,已知抛物线y=ax2+bx+c的图象与x轴交于A(2,0),B(﹣8,0)两点,与y轴交于点C(0,﹣8).
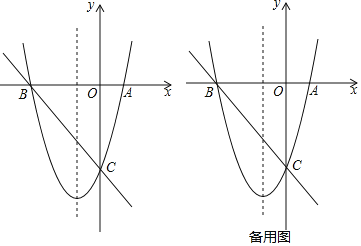
(1)求抛物线的解析式;
(2)点F是直线BC下方抛物线上的一点,当△BCF的面积最大时,求出点F的坐标;
(3)在(2)的条件下,是否存在这样的点Q(0,m),使得△BFQ为等腰三角形?如果有,请直接写出点Q的坐标;如果没有,请说明理由.
【答案】(1)y=![]() x2+3x﹣8;(2)点F的坐标是F(﹣4,﹣12);(3)点Q有坐标为(0,4
x2+3x﹣8;(2)点F的坐标是F(﹣4,﹣12);(3)点Q有坐标为(0,4![]() )或(0,﹣4
)或(0,﹣4![]() )或(0,﹣4)或(0,0).
)或(0,﹣4)或(0,0).
【解析】
(1)将A,B,C的坐标代入函数y=ax2+bx+c即可;
(2)如图1中,作FN∥y轴交BC于N,求出直线BC的解析式,设F(m,![]() m2+3m﹣8),则N(m,﹣m﹣8),再用含m的代数式表示出△BCF的面积,用函数的思想即可推出结论;
m2+3m﹣8),则N(m,﹣m﹣8),再用含m的代数式表示出△BCF的面积,用函数的思想即可推出结论;
(3)此问要分BQ=BF,QB=QF,FB=FQ三种情况进行讨论,分别用勾股定理可求出m的值,进一步写出点Q的坐标.
(1)将A(2,0),B(﹣8,0)C(0,﹣8)代入函数y=ax2+bx+c,
得, 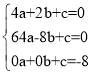
解得,![]() ,
,
∴抛物线解析式为y=![]() x2+3x﹣8;
x2+3x﹣8;
(2)如图1中,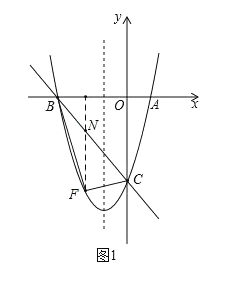
作FN∥y轴交BC于N,
将B(﹣8,0)代入y=kx﹣8,
得,k=﹣1,
∴yBC=﹣x﹣8,
设F(m,![]() m2+3m﹣8),则N(m,﹣m﹣8),
m2+3m﹣8),则N(m,﹣m﹣8),
∴S△FBC=S△FNB+S△FNC
=![]() FN×8
FN×8
=4FN
=4[(﹣m﹣8)﹣(![]() m2+3m﹣8)]
m2+3m﹣8)]
=﹣2m2﹣16m
=﹣2(m+4)2+32,
∴当m=﹣4时,△FBC的面积有最大值,
此时F(﹣4,﹣12),
∴点F的坐标是F(﹣4,﹣12);
(3)存在点Q(0,m),使得△BFQ为等腰三角形,理由如下:
①如图2﹣1,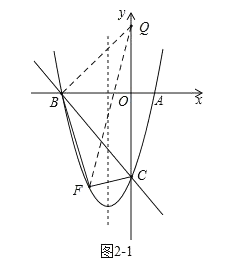
当BQ=BF时,
由题意可列,82+m2=(8﹣4)2+122,
解得,m1=![]() ,m2=
,m2=![]()
∴Q1(0,![]() ),Q2(0,
),Q2(0,![]() );
);
②如图2﹣2,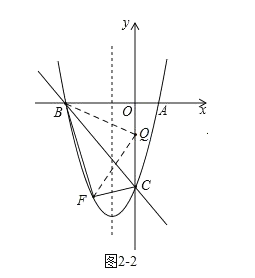
当QB=QF时,
由题意可列,82+m2=(m+12)2+42,
解题,m=﹣4,
∴Q3(0,﹣4);
③如图2﹣3,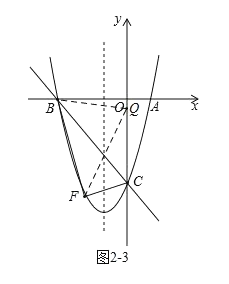
当FB=FQ时,
由题意可列,(8﹣4)2+122=(m+12)2+42,
解得,m1=0,m2=﹣24,
∴Q4(0,0),Q5(0,﹣24);
设直线BF的解析式为y=kx+b,
将B(﹣8,0),F(﹣4,﹣12)代入,
得![]() ,
,
解得,k=﹣3,b=﹣24,
∴yBF=﹣3x﹣24,
当x=0时,y=﹣24,
∴点B,F,Q重合,故Q5舍去,
∴点Q有坐标为(0,4![]() )或(0,﹣4
)或(0,﹣4![]() )或(0,﹣4)或(0,0).
)或(0,﹣4)或(0,0).


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案科目:初中数学 来源: 题型:
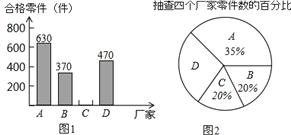
【题目】为响应国家的“一带一路”经济发展战略,树立品牌意识,我市质检部门对A、B、C、D四个厂家生产的同种型号的零件共2000件进行合格率检测,通过检测得出C厂家的合格率为95%,并根据检测数据绘制了如图1、图2两幅不完整的统计图.
(1)抽查D厂家的零件为 件,扇形统计图中D厂家对应的圆心角为 ;
(2)抽查C厂家的合格零件为 件,并将图1补充完整;
(3)通过计算说明合格率排在前两名的是哪两个厂家;
(4)若要从A、B、C、D四个厂家中,随机抽取两个厂家参加德国工业产品博览会,请用“列表法”或“画树形图”的方法求出(3)中两个厂家同时被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,且OD=OC.
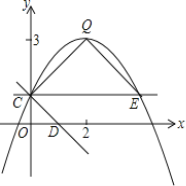
(1)求直线CD的解析式;
(2)求抛物线的解析式;
(3)将直线CD绕点C逆时针方向旋转45°所得直线与抛物线相交于另一点E,求证:△CEQ∽△CDO;
(4)在(3)的条件下,若点P是线段QE上的动点,点F是线段OD上的动点,问:在P点和F点移动过程中,△PCF的周长是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
将一个多位自然数分解为个位与个位之前的数,让个位之前的数减去个位数的两倍,若所得之差能被7整除,则原多位自然数一定能被7整除.也称这个数为“要塞数”.例如:将数1078分解为8和107,107﹣8×2=91,因为91能被7整除,所以1078能被7整除,就称1078为“要塞数”.
完成下列问题:
(1)若一个三位自然数是“要塞数”,且个位数字和百位数字都是7,则这个三位自然数位 ;
(2)若一个四位自然数M是“要塞数”,设M的个位数字为x,十位数字为y,且个位数字与百位数字的和为13,十位数字与千位数字的和也为13,记F(M)=|x﹣y|,求F(M)的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①b2﹣4ac>0;②abc>0;③a+c>0;④9a+3b+c<0.其中,正确的结论有( )
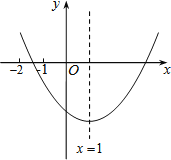
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
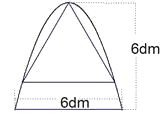
【题目】如图,有一块铁片下脚料,其外轮廓中的曲线是抛物线的一部分,要裁出一个等边三角形,使其一个顶点与抛物线的顶点重合,另外两个顶点在抛物线上,求这个等边三角形的边长(结果精确到![]() ,
,![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是“用三角板画圆的切线”的画图过程.
如图1,已知圆上一点A,画过A点的圆的切线.
![]()

画法:(1)如图2,将三角板的直角顶点放在圆上任一点C(与点A不重合)处,使其一直角边经过点A,另一条直角边与圆交于B点,连接AB;
(2)如图3,将三角板的直角顶点与点A重合,使一条直角边经过点B,画出另一条直角边所在的直线AD.
所以直线AD就是过点A的圆的切线.
请回答:该画图的依据是_______________________________________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com