
【题目】已知关于x的一元二次方程x2-(2k+1)x+k2+k=0.
(1)求证:方程有两个不相等的实数根;
(2)若△ABC的两边AB,AC的长是这个方程的两个实数根,第三边BC的长为5,当△ABC是等腰三角形时,求k的值.
【答案】(1)证明见解析(2)k的值为5或4.
【解析】试题分析:(1)先计算出△=1,然后根据判别式的意义即可得到结论;
(2)先利用公式法求出方程的解为x1=k,x2=k+1,然后分类讨论:AB=k,AC=k+1,当AB=BC或AC=BC时△ABC为等腰三角形,然后求出k的值.
试题解析:(1)证明:∵△=(2k+1)2﹣4(k2+k)=1>0,
∴方程有两个不相等的实数根;
(2)解:一元二次方程x2﹣(2k+1)x+k2+k=0的解为x=![]() ,即x1=k,x2=k+1,
,即x1=k,x2=k+1,
∵k<k+1,
∴AB≠AC.
当AB=k,AC=k+1,且AB=BC时,△ABC是等腰三角形,则k=5;
当AB=k,AC=k+1,且AC=BC时,△ABC是等腰三角形,则k+1=5,解得k=4,
综合上述,k的值为5或4.


科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP,CP的延长线分别交AD于点E,F,连结BD,DP,BD与CF相交于点H.给出下列结论: ①△ABE≌△DCF;②△DPH是等腰三角形;③PF= ![]() AB;④
AB;④ ![]() =
= ![]() .
.
其中正确结论的个数是( )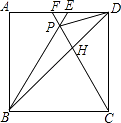
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车开往距离出发地180千米的目的地,出发后第一小时内按原计划的速度匀速行驶,一小时后以原来速度的1.5倍匀速行驶,并比原计划提前40分到达目的地.求前一小时的行驶速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】购买单价为a元的物品10个,付出b元(b>10a),应找回( )
A. (b﹣a)元 B. (b﹣10)元 C. (10a﹣b)元 D. (b﹣10a)元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将抛物线y=3x2+1向左平移1个单位,再向下平移3个单位,则所得抛物线为( )
A. y=3(x+1)2+2B. y=3(x+1)2﹣2
C.y=3(x﹣3)2+1D.y=3(x﹣3)2﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2-(2m+1)x+m2+m-2与x轴交于A、B两点,点A在点B的左边,与y轴交于点C,P(s,t)为抛物线上A、B之间一点(不包括A、B),连接AP、BP分别交y轴于点E、D
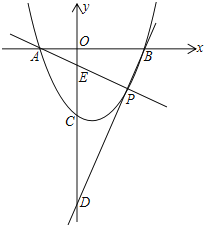
(1)若m=-1,求A、B两点的坐标
(2)若s=1,求ED的长度
(3)若∠BAP=∠ODP,求t的值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com