
ΓΨΧβΡΩΓΩΘ®1Θ©ΓΨ÷ΛΖ®ΜΊΙΥΓΩ÷ΛΟςΘΚ»ΐΫ«–Έ÷–ΈΜœΏΕ®άμΘ°
“―÷ΣΘΚ»γΆΦ1Θ§DE «ΓςABCΒΡ÷–ΈΜœΏΘ°
«σ÷ΛΘΚΓΓ ΓΓΘ°
÷ΛΟςΘΚΧμΦ”Η®÷ζœΏΘΚ»γΆΦ1Θ§‘ΎΓςABC÷–Θ§―”≥ΛDE Θ®DΓΔEΖ÷±π «ABΓΔACΒΡ÷–ΒψΘ©ΒΫΒψFΘ§ ΙΒΟEF=DEΘ§Ν§Ϋ”CFΘΜ
«κΦΧ–χΆξ≥…÷ΛΟςΙΐ≥ΧΘΚ

Θ®2Θ©ΓΨΈ ΧβΫβΨωΓΩ
»γΆΦ2Θ§‘Ύ’ΐΖΫ–ΈABCD÷–Θ§EΈΣADΒΡ÷–ΒψΘ§GΓΔFΖ÷±πΈΣABΓΔCD±Ώ…œΒΡΒψΘ§»τAG=2Θ§DF=3Θ§ΓœGEF=90ΓψΘ§«σGFΒΡ≥ΛΘ°
Θ®3Θ©ΓΨΆΊ’Ι―–ΨΩΓΩ
»γΆΦ3Θ§‘ΎΥΡ±Ώ–ΈABCD÷–Θ§ΓœA=105ΓψΘ§ΓœD=120ΓψΘ§EΈΣADΒΡ÷–ΒψΘ§GΓΔFΖ÷±πΈΣABΓΔCD±Ώ…œΒΡΒψΘ§»τAG=![]() Θ§DF=2Θ§ΓœGEF=90ΓψΘ§«σGFΒΡ≥ΛΘ°
Θ§DF=2Θ§ΓœGEF=90ΓψΘ§«σGFΒΡ≥ΛΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©DEΓΈBCΘ§DE=![]() BC,÷ΛΟςΦϊΫβΈω;Θ®2Θ©5; (3)
BC,÷ΛΟςΦϊΫβΈω;Θ®2Θ©5; (3) ![]() Θ°
Θ°
ΓΨΫβΈωΓΩΘ®1Θ©Ζ÷ΈωΘΚΗυΨί»ΐΫ«–ΈΒΡ÷–ΈΜœΏΕ®άμΧν–¥Φ¥Ω…ΘΜάϊ”ΟΓΑ±ΏΫ«±ΏΓ±÷ΛΟςΓςADEΚΆΓςCFE»ΪΒ»Θ§ΗυΨί»ΪΒ»»ΐΫ«–ΈΕ‘”ΠΫ«œύΒ»Ω…ΒΟΓœA=ΓœECFΘ§»ΪΒ»»ΐΫ«–ΈΕ‘”Π±ΏœύΒ»Ω…ΒΟAD=CFΘ§»ΜΚσ«σ≥ωΥΡ±Ώ–ΈBCFD «ΤΫ––ΥΡ±Ώ–ΈΘ§ΗυΨίΤΫ––ΥΡ±Ώ–ΈΒΡ–‘÷ ÷ΛΟςΦ¥Ω…Θ°(2)”…Θ§’ΐΖΫ–Έ–‘÷ ΦΑEΈΣAD ÷–ΒψΒΟ≥ωΓςADEΓ’ΓςCFEΘ§”…»ΪΒ»»ΐΫ«–ΈΆΤ≥ωΘ§EF¥Ι÷±ΤΫΖ÷GHΘ§¥”Εχ«σΫβ.(3) ΙΐΒψDΉςABΒΡΤΫ––œΏΫΜGEΒΡ―”≥ΛœΏ”ΎΒψHΘ§ΙΐHΉςCDΒΡ¥ΙœΏΘ§¥ΙΉψΈΣPΘ§Ν§Ϋ”HFΘ§Ω…÷ΛΟςΓςAEGΓ’ΓςDEHΘ§ΫαΚœΧθΦΰΩ…ΒΟΒΫΓςHPDΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§Ω…«σΒΟPFΒΡ≥ΛΘ§‘ΎRtΓςHFP÷–Θ§Ω…«σΒΟHFΘ§‘ρΩ…«σΒΟGFΒΡ≥ΛΘ°
Ȯ1ȩDEøBCȧDE=![]() BC
BC
÷ΛΟςΘΚ‘ΎΓςADEΚΆΓςCFE÷–Θ§ 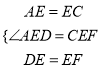 Θ§ΓύΓςADEΓ’ΓςCFEΘ®SASΘ©Θ§
Θ§ΓύΓςADEΓ’ΓςCFEΘ®SASΘ©Θ§
ΓύΓœA=ΓœECFΘ§AD=CFΘ§ΓύCFΓΈABΘ§”÷ΓΏAD=BDΘ§ΓύCF=BDΘ§
ΓύΥΡ±Ώ–ΈBCFD «ΤΫ––ΥΡ±Ώ–ΈΘ§ΓύDEΓΈBCΘ§DE=![]() BCΘ°
BCΘ°
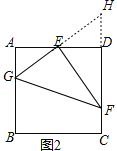
Θ®2Θ©»γΆΦ2Θ§―”≥ΛGEΓΔFDΫΜ”ΎΒψHΘ§
ΓΏEΈΣAD÷–ΒψΘ§
ΓύEA=EDΘ§«“ΓœA=ΓœEDH=90ΓψΘ§
‘ΎΓςAEGΚΆΓςDEH÷–
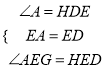 ΓύΓςAEGΓ’ΓςDEHΘ®ASAΘ©Θ§
ΓύΓςAEGΓ’ΓςDEHΘ®ASAΘ©Θ§
ΓύAG=HD=2Θ§EG=EHΘ§ΓΏΓœGEF=90ΓψΘ§ΓύEF¥Ι÷±ΤΫΖ÷GHΘ§
ΓύGF=HF=DH+DF=2+3=5ΘΜ
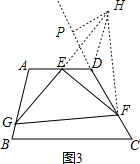
Θ®3Θ©»γΆΦ3Θ§ΙΐΒψDΉςABΒΡΤΫ––œΏΫΜGEΒΡ―”≥ΛœΏ”ΎΒψHΘ§ΙΐHΉςCDΒΡ¥ΙœΏΘ§¥ΙΉψΈΣPΘ§Ν§Ϋ”HFΘ§
Ά§Θ®1Θ©Ω…÷ΣΓςAEGΓ’ΓςDEHΘ§GF=HFΘ§ΓύΓœA=ΓœHDE=105ΓψΘ§AG=HD=![]() Θ§
Θ§
ΓΏΓœADC=120ΓψΘ§ΓύΓœHDF=360Γψ©¹105Γψ©¹120Γψ=135ΓψΘ§
ΓύΓœHDP=45ΓψΘ§ΓύΓςPDHΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§
ΓύPD=PH=3Θ§ΓύPF=PD+DF=3+2=5Θ§
‘ΎRtΓςHFP÷–Θ§ΓœHPF=90ΓψΘ§HP=3Θ§PF=5Θ§
ΓύHF=![]() ==
==![]() ΓύGF=
ΓύGF=![]() Θ°
Θ°
ΒψΨΠ;±ΨΧβΩΦ≤ιΝΥΥΡ±Ώ–ΈΒΡΉέΚœ”Π”ΟΘ§ΩΦ≤ιΝΥ’ΐΖΫ–ΈΒΡ–‘÷ Θ§»ΪΒ»»ΐΫ«–ΈΒΡ≈–Ε®ΚΆ–‘÷ Θ§Β»―ϋ»ΐΫ«–ΈΒΡ–‘÷ Θ§Ι¥Ι…Ε®άμΘΜ±ΨΧβΩΦ≤ι÷Σ ΕΒψΫœΕύΉέΚœ–‘Ϋœ«ΩΘ§Ρ―Ε»Ϋœ¥σ.


 Οϊ–ΘΩΈΧΟœΒΝ–¥πΑΗ
Οϊ–ΘΩΈΧΟœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
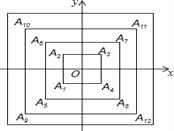
ΓΨΧβΡΩΓΩ»γΆΦΘ§’ΐΖΫ–ΈA1A2A3A4Θ§A5A6A7A8Θ§A9A10A11A12Θ§Γ≠Θ§Θ®ΟΩΗω’ΐΖΫ–Έ¥”ΒΎ»ΐœσœόΒΡΕΞΒψΩΣ ΦΘ§Α¥Υ≥ ±’κΖΫœρΥ≥–ρΘ§“ά¥ΈΦ«ΈΣA1Θ§A2Θ§A3Θ§A4ΘΜA5Θ§A6Θ§A7Θ§A8ΘΜA9Θ§A10Θ§A11Θ§A12ΘΜΓ≠Θ©’ΐΖΫ–ΈΒΡ÷––ΡΨυ‘ΎΉχ±ξ‘≠ΒψOΘ§Ης±ΏΨυ”κx÷αΜρy÷αΤΫ––Θ§»τΥϋΟ«ΒΡ±Ώ≥Λ“ά¥Έ «2Θ§4Θ§6Θ§Γ≠Θ§‘ρΕΞΒψA2016ΒΡΉχ±ξΈΣ_____.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
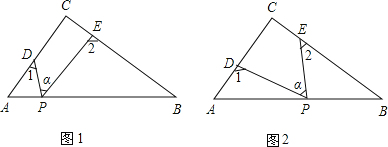
ΓΨΧβΡΩΓΩRtΓςABC÷–Θ§ΓœC=90ΓψΘ§ΒψDΓΔEΖ÷±π «ΓςABC±ΏACΓΔBC…œΒΡΒψΘ§ΒψP «“ΜΕ·Βψ.ΝνΓœPDA=Γœ1Θ§ΓœPEB=Γœ2Θ§ΓœDPE=ΓœΠΝ.
Θ®1Θ©»τΒψP‘ΎœΏΕΈAB…œΘ§»γΆΦΘ®1Θ©Υυ ΨΘ§«“ΓœΠΝ=50ΓψΘ§‘ρΓœ1+Γœ2=ΓΓ ΓΓΓψΘΜ
Θ®2Θ©»τΒψP‘Ύ±ΏAB…œ‘ΥΕ·Θ§»γΆΦΘ®2Θ©Υυ ΨΘ§‘ρΓœΠΝΓΔΓœ1ΓΔΓœ2÷°ΦδΒΡΙΊœΒΈΣΘΚΓΓ ΓΓΘΜ
Θ®3Θ©»τΒψP‘ΥΕ·ΒΫ±ΏABΒΡ―”≥ΛœΏ…œΘ§»γΆΦΘ®3Θ©Υυ ΨΘ§‘ρΓœΠΝΓΔΓœ1ΓΔΓœ2÷°Φδ”–ΚΈΙΊœΒΘΩ≤¬œκ≤ΔΥΒΟςάμ”….
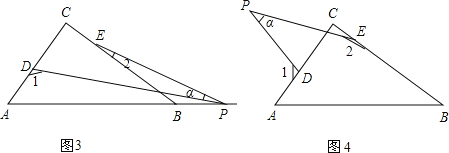
Θ®4Θ©»τΒψP‘ΥΕ·ΒΫΓςABC–ΈΆβΘ§»γΆΦΘ®4Θ©Υυ ΨΘ§‘ρΓœΠΝΓΔΓœ1ΓΔΓœ2÷°ΦδΒΡΙΊœΒΈΣΘΚΓΓΓΓ.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΦΉΓΔ““ΝΫ…Χ≥ΓΉ‘––Ε®Φέœζ έΡ≥“Μ…ΧΤΖΘ°
Θ®1Θ©ΦΉ…Χ≥ΓΫΪΗΟ…ΧΤΖΧαΦέ25%ΚσΒΡ έΦέΈΣ1.25‘ΣΘ§‘ρΗΟ…ΧΤΖ‘ΎΦΉ…Χ≥ΓΒΡ‘≠ΦέΈΣΓΓ ΓΓ‘ΣΘΜ
Θ®2Θ©““…Χ≥ΓΕ®Φέ”–ΝΫ÷÷ΖΫΑΗΘΚΖΫΑΗΫΪΗΟ…ΧΤΖΧαΦέ20%ΘΜΖΫΑΗΫΪΗΟ…ΧΤΖΧαΦέ1‘ΣΓΘΡ≥ΙΥΩΆΖΔœ÷‘Ύ““…Χ≥Γ”Ο60‘Σ«°ΙΚ¬ρΗΟ…ΧΤΖΘ§Α¥ΖΫΑΗΙΚ¬ρΒΡΦΰ ΐ «Α¥ΖΫΑΗΙΚ¬ρΒΡΦΰ ΐΒΡ2±Ε…Ό10ΦΰΘ§«σΗΟ…ΧΤΖ‘Ύ““…Χ≥ΓΒΡ‘≠Φέ «Εύ…ΌΘΩ
Θ®3Θ©ΦΉΓΔ““ΝΫ…Χ≥ΓΑ―ΗΟ…ΧΤΖΨυΑ¥‘≠ΦέΫχ––ΝΥΝΫ¥ΈΦέΗώΒς’ϊΘ°ΦΉ…Χ≥ΓΘΚΒΎ“Μ¥ΈΧαΦέΒΡΑΌΖ÷¬ «aΘ§ΒΎΕΰ¥ΈΧαΦέΒΡΑΌΖ÷¬ «bΘΜ““…Χ≥ΓΘΚΝΫ¥ΈΧαΦέΒΡΑΌΖ÷¬ ΕΦ «![]() Θ®aΘΨ0Θ§bΘΨ0Θ§aΓΌbΘ©Θ°«κΈ ΦΉΓΔ““ΝΫ…Χ≥ΓΘ§ΡΡΗω…Χ≥ΓΒΡΧαΦέΫœΕύΘΩ«κΥΒΟςάμ”…Θ°
Θ®aΘΨ0Θ§bΘΨ0Θ§aΓΌbΘ©Θ°«κΈ ΦΉΓΔ““ΝΫ…Χ≥ΓΘ§ΡΡΗω…Χ≥ΓΒΡΧαΦέΫœΕύΘΩ«κΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΒψNΒΡΉχ±ξΈΣ(aΘ§aΘ≠1)Θ§‘ρΒψN“ΜΕ®≤Μ‘ΎΒΎ________œσœόΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩœ¬Ν–ΖΫ≥Χ”–ΝΫΗωœύΒ»ΒΡ Β ΐΗυΒΡ «( )
A. x2ΘΪxΘΪ1ΘΫ0 B. 4x2ΘΪ2xΘΪ1ΘΫ0 C. x2ΘΪ12xΘΪ36ΘΫ0 D. x2ΘΪxΘ≠2ΘΫ0
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§Γ―O «ΓςABCΒΡΆβΫ”‘≤Θ§“―÷ΣADΤΫΖ÷ΓœBACΫΜΓ―O”ΎΒψDΘ§Ν§ΫαCDΘ§―”≥ΛACΘ§BDΘ§œύΫΜ”ΎΒψF.œ÷Ηχ≥ωœ¬Ν–Ϋα¬έΘΚ
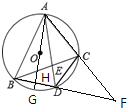
ΔΌ»τAD=5Θ§BD=2Θ§‘ρDE=![]() ΘΜ
ΘΜ
ΔΎ![]() ΘΜ
ΘΜ
Δέ![]() ΓΉ
ΓΉ![]() ΘΜ
ΘΜ
Δή»τ÷±ΨΕAGΓΆBDΫΜBD”ΎΒψHΘ§AC=FC=4Θ§DF=3Θ§‘ρcosF=![]() ΘΜ
ΘΜ
‘ρ’ΐ»ΖΒΡΫα¬έ «Θ® Θ©
AΘ°ΔΌΔέ B.ΔΎΔέΔή C.ΔέΔή D.ΔΌΔΎΔή
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥ΙΪΥΨ»ΞΡξ1-3‘¬ΤΫΨυΩςΥπ1.5Άρ‘ΣΘ§4-6‘¬ΤΫΨυ”·άϊ2Άρ‘ΣΘ§7-10‘¬ΤΫΨυΟΩ‘¬”·άϊ1.7Άρ‘ΣΘ§11-12‘¬ΤΫΨυΟΩ‘¬ΩςΥπ2.3Άρ‘ΣΘ§’βΗωΙΪΥΨ»ΞΡξ”·Ως«ιΩω «_________.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΧΫΥςΙφ¬…ΘΚ71=7Θ§72=49Θ§73=343Θ§74=2401Θ§75=16807Θ§Γ≠Ρ«Ο¥72007+1ΒΡΗωΈΜ ΐΉ÷ «Θ®ΓΓΓΓΘ©
A. 8 B. 4 C. 2 D. 0
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com