
【题目】如图所示,AB是![]() 直径,
直径,![]() 弦BC于点F,且交
弦BC于点F,且交![]() 于点E,且∠AEC=∠ODB.
于点E,且∠AEC=∠ODB.
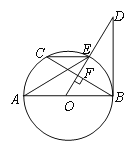
(1)判断直线![]() 和
和![]() 的位置关系,并给出证明;
的位置关系,并给出证明;
(2)当![]() ,
,![]() 时,求
时,求![]() 的面积.
的面积.
【答案】(1)直线![]() 和
和![]() 的位置关系是相切.证明见解析;(2)
的位置关系是相切.证明见解析;(2)![]() 的面积是
的面积是![]() .
.
【解析】
(1)直线BD和⊙O的位置关系是相切,理由是由∠AEC=∠ABC,∠AEC=∠ODB,得到∠ABC=∠ODB,求出∠BOD+∠D=90°,推出∠OBD=90°,即可得到
(2)根据垂径定理得出BF=CF=![]() BC=4,连接AC,由AB是圆的直径得到∠ACB=∠DFB=90°,证出△ACB∽△BED,根据相似三角形的性质得到
BC=4,连接AC,由AB是圆的直径得到∠ACB=∠DFB=90°,证出△ACB∽△BED,根据相似三角形的性质得到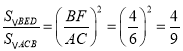 ,求出△ABC的面积,即可求出△DFB的面积.
,求出△ABC的面积,即可求出△DFB的面积.
(1)答:直线BD和⊙O的位置关系是相切,
证明:∵∠AEC=∠ABC,∠AEC=∠ODB,
∴∠ABC=∠ODB,
∵OD⊥弦BC,
∴∠OFB=90°,
∴∠DOB+∠ABC=90°,
∴∠BOD+∠D=90°,
∴∠OBD=180°-90°=90°,
∵OB是半径,
∴直线BD是圆O的切线,
即直线BD和⊙O的位置关系是相切;
(2)解:∵![]() ,
,![]() 是圆
是圆![]() 的半径,
的半径,![]() ,
,
∴![]() ,
,![]() ,连接
,连接![]() ,
,
∵![]() 是圆的直径,
是圆的直径,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴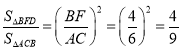 ,
,
∵![]() 的面积是
的面积是![]() ,
,
∴![]() 的面积是
的面积是![]() ,
,
答:![]() 的面积是
的面积是![]() .
.


科目:初中数学 来源: 题型:
【题目】两个边长分别为![]() 和
和![]() 的正方形如图放置(图1),其未叠合部分(阴影)面积为
的正方形如图放置(图1),其未叠合部分(阴影)面积为![]() ;若再在图1中大正方形的右下角摆放一个边长为
;若再在图1中大正方形的右下角摆放一个边长为![]() 的小正方形(如图2),两个小正方形叠合部分(阴影)面积为
的小正方形(如图2),两个小正方形叠合部分(阴影)面积为![]() .
.



(1)用含![]() 、
、![]() 的代数式分别表示
的代数式分别表示![]() 、
、![]() ;
;
(2)若![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)当![]() 时,求出图3中阴影部分的面积
时,求出图3中阴影部分的面积![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】襄阳卧龙大桥横跨汉江,是我市标志性建筑之一.某校数学兴趣小组在假日对竖立的索塔在桥面以上的部分(上塔柱BC和塔冠BE)进行了测量.如图所示,最外端的拉索AB的底端A到塔柱底端C的距离为121m,拉索AB与桥面AC的夹角为37°,从点A出发沿AC方向前进23.5m,在D处测得塔冠顶端E的仰角为45°.请你求出塔冠BE的高度(结果精确到0.1m.参考数据sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,![]() ≈1.41).
≈1.41).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校初二学生每周上网的时间,两位学生进行了抽样调查.小丽调查了初二电脑爱好者中40名学生每周上网的时间;小杰从全校400名初二学生中随机抽取了40名学生,调查了每周上网的时间.小丽与小杰整理各自样本数据,如下表所示:
时间段 (小时/周) | 小丽抽样 人数 | 小杰抽样 人数 |
0~1 | 6 | 22 |
1~2 | 10 | 10 |
2~3 | 16 | 6 |
3~4 | 8 | 2 |
(每组可含最低值,不含最高值)
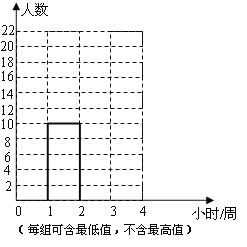
(1)你认为哪位同学抽取的样本不合理?请说明理由;
(2)根据合理抽取的样本,把上图中的频数分布直方图补画完整;
(3)专家建议每周上网2小时以上(含2小时)的同学应适当减少上网的时间,估计该校全体初二学生中有多少名同学应适当减少上网的时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据某网站调查,2019年网民最关注的热点话题分别是:消费、教育、环保、反腐及其他共五类,根据调查的部分相关数据绘制的统计图如图:
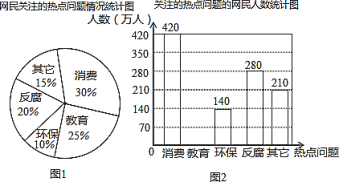
根据以上信息解答下列问题:
(1)请补全条形图,并在图中标明相应数据.
(2)若某市中心城区约有90万人口,请你估计该市中心城区最关注教育问题的人数约有多少万人?
(3)据统计,2017年网民最关注教育问题的人数所占百分比约为10%,则从2017年到2019年关注该问题网民数的年平均增长率约为多少?(已知2017~2019年每年接受调查的网民人数相同,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,在△ABC中,DE是边AB的垂直平分线,分别交边AB,AC于点D,E,连接BE,点F在边AC上,AB=AF,连接BF.
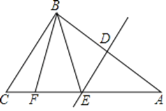
(1)求证:∠BEC=2∠A;
(2)当∠BFC=108°时,求∠A的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com