
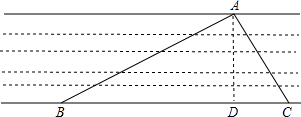
 计算出河宽AD.(结果用根式表示)
计算出河宽AD.(结果用根式表示)  新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:
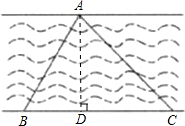 为了测量汉江某段河面的宽度,秋实同学设计了如下图所示的测量方案:先在河的北岸选一定点A,再在河的南岸选定相距a米的两点B、C(如图),分别测得∠ABC=α,∠ACB=β,请你根据秋实同学测得的数据,计算出河宽AD.(结果用含a和含α、β的三角函数表示)
为了测量汉江某段河面的宽度,秋实同学设计了如下图所示的测量方案:先在河的北岸选一定点A,再在河的南岸选定相距a米的两点B、C(如图),分别测得∠ABC=α,∠ACB=β,请你根据秋实同学测得的数据,计算出河宽AD.(结果用含a和含α、β的三角函数表示)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
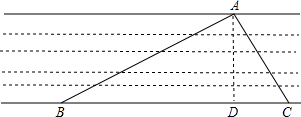 计算出河宽AD.(结果用根式表示)
计算出河宽AD.(结果用根式表示)查看答案和解析>>
科目:初中数学 来源:第25章《解直角三角形》中考题集(40):25.3 解直角三角形(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2008年福建省南平市剑津中学九年级毕业班检测数学试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com