练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．下列各命题不成立的是（　　）
    A．平行四边形的对边平行且相等
    B．依次连结正方形各边中点所得的四边形是正方形
    C．对角线互相平分且相等的四边形是矩形
    D．对角线互相垂直平分的四边形是正方形

    分析 根据各个选项中的说法可以判断各命题是否成立，从而可以解答本题．

    解答 解：平行四边形的对边平行且相等，故选项A正确，
    依次连结正方形各边中点所得的四边形是正方形，故选项B正确，
    对角线互相平分且相等的四边形是矩形，故选项C正确，
    对角线互相垂直平分的四边形是菱形，但不一定是正方形，故选项D错误，
    故选D．

    点评 本题考查命题与定理，解答本题的关键是明确题意，可以判断各个选项中的命题是否成立．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    8．（1）解方程：$\frac{x}{x-1}$-$\frac{3}{1-x}$=2
    （2）解不等式组：$\left\{\begin{array}{l}{2x-1＞-3}\\{8-2x≤x-1}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．计算：-12016-|-2$\sqrt{3}}$|+$\sqrt{12}$•tan60°+（-$\frac{1}{3}}$）-2•tan30°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

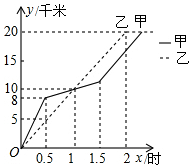    8．在20km越野赛中，甲乙两选手的行程y（单位：km）随时间x（单位：h）变化的图象如图所示，根据图中提供的信息，有下列说法：
    ①两人相遇前，甲的速度小于乙的速度；
    ②出发后1小时，两人行程均为10km；
    ③出发后1.5小时，甲的行程比乙多3km；
    ④甲比乙先到达终点．
    其中正确的有3个．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．先化简，再求值：（$\frac{x}{x-1}$+$\frac{2x}{x+1}$）÷$\frac{x}{{x}^{2}-1}$，其中x=$\frac{2}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

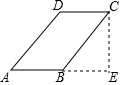    5．作平行四边形ABCD的高CE，B是AE的中点，如图．
    （1）小琴说：如果连接DB，则DB⊥AE，对吗？说明理由．
    （2）如果BE：CE=1：$\sqrt{2}$，BC=3cm，求AB．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．下列四个等式从左到右的变形，是多项式的因式分解的是（　　）
    A．（x+3）（x-3）=x2-9B．a2b+ab2=ab（a+b）
    C．x2-3x+1=x（x-3）+1D．${m^2}-2m-1=m（m-2-\frac{1}{m}）$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．北盘江旅游景点在2017年6月4日至6月14日蓄水期间，水位由106米直升至135米，是划船旅游最佳的时期，设水位匀速上生，那么下列图象中，能反应这10天水位h（米）随时间t（天）变化的是（　　）
    A．B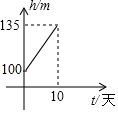．C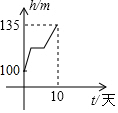．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

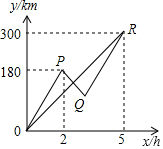    10．已知A，B两地公路长300km，甲、乙两车同时从A地出发沿同一公路驶往B地，2小时后，甲车接到电话需返回这条公路上的C处取回货物，于是甲车立即原路返回C，取了货物又立即赶往B地（取货物的时间忽略不计），结果两车同时到达B地．两车的速度始终保持不变，设两车出发x小时后，甲、乙距离A地的距离分别为y1（km）和y2（km），它们的函数图象分别是折线OPQR和线段OR．
    （1）求甲、乙两车的速度．
    （2）求A，C两地之间的距离．
    （3）甲、乙两车在途中相遇时，距离A地多远？

    查看答案和解析>>

    同步练习册答案