
【题目】如图,矩形ABCD中,∠ACB=30°,将一块直角三角板的直角顶点P放在两对角线AC,BD的交点处,以点P为旋转中心转动三角板,并保证三角板的两直角边分别于边AB,BC所在的直线相交,交点分别为E,F.
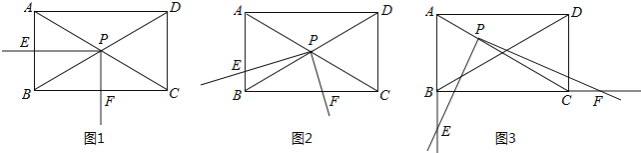
(1)当PE⊥AB,PF⊥BC时,如图1,则![]() 的值为 ;
的值为 ;
(2)现将三角板绕点P逆时针旋转α(0°<α<60°)角,如图2,求![]() 的值;
的值;
(3)在(2)的基础上继续旋转,当60°<α<90°,且使AP:PC=1:2时,如图3,![]() 的值是否变化?证明你的结论.
的值是否变化?证明你的结论.
【答案】解:(1)![]() 。
。
(2)如答图1,过点P作PM⊥AB于点M,PN⊥BC于点N,则PM⊥PN。
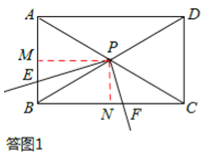
∵PM⊥PN,PE⊥PF,∴∠EPM=∠FPN。
又∵∠PME=∠PNF=90°,∴△PME∽△PNF。
∴![]() 。
。
由(1)知,![]() ,
,
∴![]() 。
。
(3)变化。证明如下:
如答图2,过点P作PM⊥AB于点M,PN⊥BC于点N,则PM⊥PN,PM∥BC,PN∥AB。
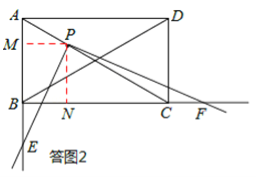
∵PM∥BC,PN∥AB,
∴∠APM=∠PCN,∠PAM=∠CPN。
∴△APM∽△PCN。
∴![]() ,得CN=2PM。
,得CN=2PM。
在Rt△PCN中,![]() ,
,
∴![]() 。
。
∵PM⊥PN,PE⊥PF,∴∠EPM=∠FPN。
又∵∠PME=∠PNF=90°,∴△PME∽△PNF。
∴![]() 。
。
∴![]() 的值发生变化
的值发生变化
【解析】
试题(1)证明△APE≌△PCF,得PE=CF;在Rt△PCF中,解直角三角形求得![]() 的值:
的值:
∵矩形ABCD,∴AB⊥BC,PA=PC。
∵PE⊥AB,BC⊥AB,∴PE∥BC。∴∠APE=∠PCF。
∵PF⊥BC,AB⊥BC,∴PF∥AB。∴∠PAE=∠CPF。
∵在△APE与△PCF中,∠PAE=∠CPF,PA=PC,∠APE=∠PCF,
∴△APE≌△PCF(ASA)。∴PE=CF。
在Rt△PCF中,![]() ,∴
,∴![]() 。
。
(2)如答图1所示,作辅助线,构造直角三角形,证明△PME∽△PNF,并利用(1)的结论,求得![]() 的值;
的值;
(3)如答图2所示,作辅助线,构造直角三角形,首先证明△APM∽△PCN,求得![]() ;然后证明△PME∽△PNF,从而由
;然后证明△PME∽△PNF,从而由![]() 求得
求得![]() 的值。与(1)(2)问相比较,
的值。与(1)(2)问相比较,![]() 的值发生了变化。
的值发生了变化。


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】小明每天早上要在7:50之前赶到距家1000 m的学校.小明每天以80 m/min的速度出发.
(1)小明出发5 min后,小明的爸爸发现他忘了带数学书.于是,爸爸立即以 180 m/min的速度去追小明,并且在途中追上了小明.爸爸追上小明用了多长时间?
(2)小明出发 8 min后,妈妈急于上班,门锁碰上时,发现忘带手机和钥匙,于是立即以120 m/min的速度去追小明拿钥匙.请问妈妈能否在小明进学校前追上小明.
查看答案和解析>>
科目:初中数学 来源: 题型:
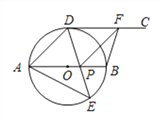
【题目】如图,AB为⊙O的直径,点D,E是位于AB两侧的半圆AB上的动点,射线DC切⊙O于点D.连接DE,AE,DE与AB交于点P,F是射线DC上一动点,连接FP,FB,且∠AED=45°.
(1)求证:CD∥AB;
(2)填空:
①若DF=AP,当∠DAE=_________时,四边形ADFP是菱形;
②若BF⊥DF,当∠DAE=_________时,四边形BFDP是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线AB分别交坐标轴于A(2,0)、B(0,-6)两点直线上任意一点P(x,y),设点P到x轴和y轴的距离分别是m和n,则m+n的最小值为( )

A.2B.3C.5D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程(x﹣3)(x﹣2)=|m|.
(1)求证:对于任意实数m,方程总有两个不相等的实数根;
(2)若方程的一个根是1,求m的值及方程的另一个根.
查看答案和解析>>
科目:初中数学 来源: 题型:
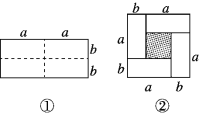
【题目】动手操作:如图①是一个长为2a,宽为2b的长方形,沿图中的虚线剪开分成四个大小相等的长方形,然后按照图②所示拼成一个正方形.
提出问题:
(1)观察图②,请用两种不同的方法表示阴影部分的面积:_____________,_____________;
(2)请写出三个代数式(a+b)2,(a-b)2,ab之间的一个等量关系:___________________________;
问题解决:根据上述(2)中得到的等量关系,解决下列问题:已知x+y=8,xy=7,求x-y的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强公民的节水意识,合理利用水资源,嘉兴某地区采用价格调控的手段达到节水的目的,该市自来水收费的收费标准如下表:
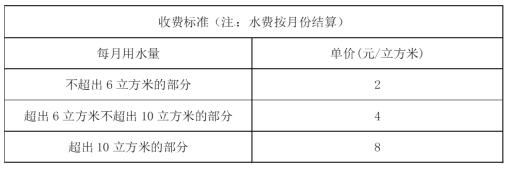
例如:某户居民1月份用水8立方米,应收水费为2×6+4×(8-6)=20(元).
请根据上表的内容解答下列问题:
(1)若某户居民2月份用水4立方米,则应收水费多少元?
(2)若某户居民3月份交水费44元,则用水量为多少立方米?
(3)若某户居民4月份用水a立方米,请用含a的代数式表示应收水费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:

(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),求W与x之间的函数表达式(利润=收入-成本);
(3)试说明(2)中总利润W随售价x的变化而变化的情况,并指出售价为多少元时获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AGF=∠ABC,∠1+∠2=180°.
(1)试判断BF与DE的位置关系,并说明理由;
(2)若BF⊥AC,∠2=150°,求∠AFG的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com