练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    6．（1）如图1，在平行四边形ABCD中，请作出一条直线，将其分成面积相等的两部分；
    （2）如图2，在多边形ABCDEF中，AB∥CD∥EF，AF∥DE∥BC，请作出一条直线，将该多边形分成面积相等的两部分．（不写作法，保留作图痕迹）

    分析 （1）由于平行四边形是中心对称图形，于是过对角线的交点作直线即可；
    （2）延长CB交EF于G，过两个平行四边形的对角线交点作直线即可．

    解答 解：（1）连接AC、BD交于点O，
    过O作直线，即把平行四边形面积等分；
    如图所示：
    （2）延长CB交EF于G，连接CE、DG交于点M，
    连接AG、BF交于点N，作直线MN，
    如图所示

    点评 本题考查了平行四边形的性质；熟练掌握平行四边形的性质是关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    19．阅读：
    我们知道，|a|=$\left\{\begin{array}{l}{a，a≥0}\\{-a，a＜0}\end{array}\right.$于是要解不等式|x-3|≤4，我们可以分两种情况去掉绝对值符号，转化为我们熟悉的不等式，按上述思路，我们有以下解法：
    解：（1）当x-3≥0，即x≥3时：x-3≤4
    解这个不等式，得：x≤7
    由条件x≥3，有：3≤x≤7
    （2）当x-3＜0，即 x＜3时，-（x-3）≤4
    解这个不等式，得：x≥-1
    由条件x＜3，有：-1≤x＜3
    ∴如图，综合（1）、（2）原不等式的解为：-1≤x≤7
    根据以上思想，请探究完成下列2个小题：
    （1）|x+1|≤2；
    （2）|x-2|≥1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．若a+b=-6，ab=6，则$\sqrt{\frac{b}{a}}$+$\sqrt{\frac{a}{b}}$的值为（　　）
    A．$\sqrt{6}$B．-$\sqrt{6}$C．2$\sqrt{3}$D．-2$\sqrt{3}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    15．如图，有一张直角三角形纸片，两直角边AC=7cm，BC=11cm，将△ABC折叠，点B与点A重合，折痕为DE，则CD的长为$\frac{36}{11}$cm．

    查看答案和解析>>

    科目：初中数学 来源：2017届广东省梅州市九年级下学期第一次月考数学试卷（解析版） 题型：判断题

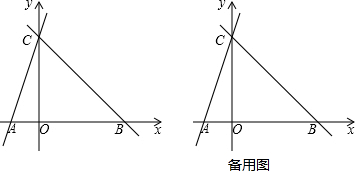
    如图，B为双曲线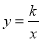（x＞0）上一点，直线AB平行于y轴交直线y=x于点A，交x轴于点D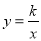， 与直线y=x交于点C，若OB2﹣AB2=4

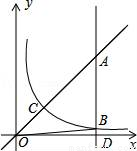
    （1）求k的值；

    （2）点B的横坐标为4时，求△ABC的面积；

    （3）双曲线上是否存在点B，使△ABC∽△AOD？若存在，求出点B的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．若关于x的不等式组$\left\{\begin{array}{l}{x-a＞2}\\{b-2x＞0}\end{array}\right.$的解集为-1＜x＜1，则（a+b）2017的值是（　　）
    A．1B．$\frac{1}{2}$C．-1D．-$\frac{1}{2}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．如图，直线y=kx+k交x轴，y轴分别于A，C，直线BC过点C交x轴于B，OC=3OA，∠CBA=45°．
    （1）求直线BC的解析式；
    （2）动点P从A出发沿射线AB匀速运动，速度为2个单位/秒，连接CP，设△PBC的面积为S，点P的运动时间为t秒，求S与t之间的函数关系式，直接写出t的取值范围；
    （3）在（2）的条件下，当点P在AB的延长线上运动时，过点O作OD⊥PC于D，交BC于点E，连接AE，当∠EAB=∠CPA时，在坐标轴上有点K，且KC=KP，求点K的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

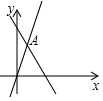    15．如图，已知函数y=3x和y=ax+5的图象相交于点A（n，3），则不等式3x＞ax+5的解集为（　　）
    A．x＜0B．x＜1C．x＞1D．x＞3

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

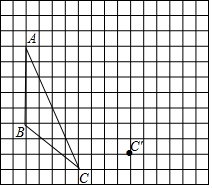    16．画图并填空，如图：方格纸中每个小正方形的边长都为1，△ABC的顶点都在方格纸的格点上，将△ABC经过一次平移后得到△A'B'C'．图中标出了点C的对应点C'．
    （1）请画出平移后的△A'B'C'；
    （2）若连接AA'，BB'，则这两条线段的关系是平行且相等；
    （3）利用网格画出△ABC中AC边上的中线BD以及AB边上的高CE；
    （4）线段AB在平移过程中扫过区域的面积为20．

    查看答案和解析>>

    同步练习册答案