
A.y=1+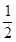 x2 x2 | B.y=(2x+1)2 | C.y=(x-1)2 | D.y=2x2 |
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 的图像经过点
的图像经过点 和点B,其中点B在第一象限,且OA=OB,cot∠BAO=2.
和点B,其中点B在第一象限,且OA=OB,cot∠BAO=2.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
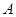 坐标为(2,4),直线x=2与
坐标为(2,4),直线x=2与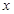 轴相交于点
轴相交于点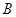 ,连结
,连结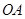 ,抛物线y=x
,抛物线y=x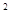
 从点
从点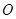 沿
沿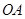 方向平移,与直线x=2交于点
方向平移,与直线x=2交于点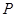 ,顶点
,顶点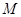 到
到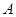 点时停止移动.
点时停止移动.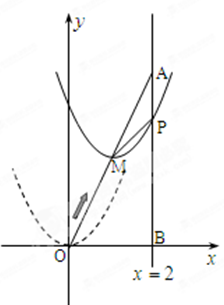
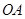 所在直线的函数解析式;
所在直线的函数解析式;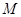 的横坐标为
的横坐标为 ,
, 的代数式表示点
的代数式表示点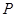 的坐标;
的坐标; 为何值时,线段
为何值时,线段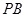 最短;
最短;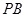 最短时,相应的抛物线上是否存在点
最短时,相应的抛物线上是否存在点 ,使△
,使△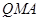 的面积与△
的面积与△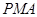 的面积相等,若存在,请求出点
的面积相等,若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
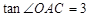 ,求抛物线的表达式;
,求抛物线的表达式;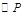 相离、相切、相交.
相离、相切、相交.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
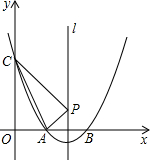

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 轴于点
轴于点 ,交
,交 轴于
轴于 ,
, 两点(点
两点(点 在点
在点 的左侧),已知
的左侧),已知 点坐标为(6,0).
点坐标为(6,0).
 作线段
作线段 的垂线交抛物线于点
的垂线交抛物线于点 ,如果以点
,如果以点 为圆心的圆与抛物线的对称轴
为圆心的圆与抛物线的对称轴 相切,先补全图形,再判断直线
相切,先补全图形,再判断直线 与⊙
与⊙ 的位置关系并加以证明;
的位置关系并加以证明; 是抛物线上的一个动点,且位于
是抛物线上的一个动点,且位于 ,
, 两点之间.问:当点
两点之间.问:当点 运动到什么位置时,
运动到什么位置时, 的面积最大?求出
的面积最大?求出 的最大面积.
的最大面积.查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
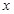 与函数值
与函数值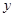 的对应值,判断方程ax2+b x+c=0(a≠0)的一个解
的对应值,判断方程ax2+b x+c=0(a≠0)的一个解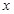 的范围是( )
的范围是( ) 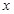 | 6.17 | 6.18 | 6.19 | 6.20 |
| y=ax2+bx+c | -0.03 | -0.01 | 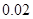 |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com