
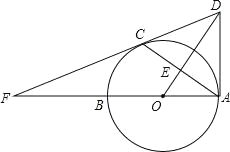
【题目】如图,已知AB是⊙O的直径,C是⊙O上的点,且OE⊥AC于点E,过点C作⊙O的切线,交OE的延长线于点D,交AB的延长线于点F,连接AD.(1)求证:AD是⊙O的切线;
(2)若cos∠BAC=![]() ,AC=8,求线段AD的长.
,AC=8,求线段AD的长.
【答案】(1)证明见解析(2)![]()
【解析】
试题分析:(1)连接OC,由切线的性质得出∠OCD=90°,由等腰三角形的性质得出∠COD=∠AOD,由SAS证明△COD≌△AOD,得出∠OAD=∠OCD=90°,即可得出结论;
(2)由直角三角形的锐角关系证出∠ODA=∠BAC,由垂径定理得出AE=CE=![]() AC=4,由三角函数得出
AC=4,由三角函数得出![]() ,设DE=4x,AD=5x,则AE=3x=4,求出x,即可得出结果.
,设DE=4x,AD=5x,则AE=3x=4,求出x,即可得出结果.
试题解析:(1)证明:连接OC,如图所示:
∵DC是⊙O的切线,
∴OC⊥DF,
∴∠OCD=90°,
∵OC=OA,OE⊥AC,
∴∠COD=∠AOD,
在△OAD和△OCD中,
 ,
,
∴△COD≌△AOD(SAS),
∴∠OAD=∠OCD=90°,
∴AD是⊙O的切线;
(2)解:∵∠OAD=90°,AC⊥OD,
∴∠ODA=∠BAC,AE=CE=![]() AC=4,
AC=4,
在Rt△ADE中,cos∠BAC=cos∠ADE=![]() ,
,
∴设DE=4x,AD=5x,
则AE=3x=4,
∴x=![]() ,
,
∴AD=![]() .
.



科目:初中数学 来源: 题型:
【题目】下列关于矩形的说法,正确的是( )
A.对角线相等的四边形是矩形
B.对角线互相平分的四边形是矩形
C.矩形的对角线相等且互相平分
D.矩形的对角线互相垂直且平分
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠A=∠C=90°,BE平分∠ABC交CD于E,DF平分∠ADC交AB于F.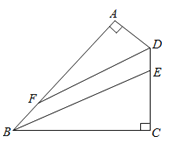
(1)若∠ABC=60°,则∠ADC= °,∠AFD=°;
(2)BE与DF平行吗?试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市地铁2号线已开工,全长约332000m,将332000科学记数法表示应为( )
A. 0.332×106 B. 3.32×105 C. 33.2×104 D. 332×103
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,正确的是( )
A. 任何有理数的偶数次方都是正数
B. 任何一个整数都有倒数
C. 若b=a,则|b|=|a|
D. 一个正数与一个负数互为相反数
查看答案和解析>>
科目:初中数学 来源: 题型:
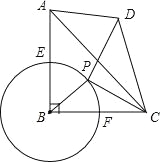
【题目】如图,在等腰直角三角形ABC中,∠ABC=90°,AB=BC=4,⊙B与AB、BC交于E、F,点P是弧EF上的一个动点,连接PC,线段PC绕P点逆时针旋转90°到PD,连接CD,AD.
(1)求证:△BPC∽△ADC;
(2)当四边形ABCD满足AD∥CB且是面积为12时,求⊙B的半径;
(3)若⊙B的半径的为2,当点P沿弧EF从点E运动至点PC与⊙B相切时,求点D的运动路径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
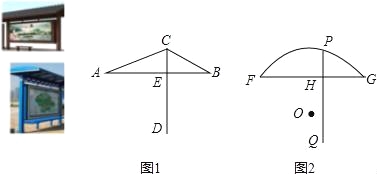
【题目】我市城市风貌提升工程正在火热进行中,检查中发现一些破旧的公交车候车亭有碍观瞻,现准备制作一批新的公交车候车亭,查看了网上的一些候车亭图片后,设计师画了两幅侧面示意图,AB,FG均为水平线段,CD⊥AB,PQ⊥FG,E,H为垂足,且AE=FH,AB=FG=2米,图1中tanA=![]() ,tanB=
,tanB=![]() ,图2点P在弧FG上.且弧FG所在圆的圆心O到FG,PQ的距离之比为5:2,
,图2点P在弧FG上.且弧FG所在圆的圆心O到FG,PQ的距离之比为5:2,
(1)求图1中的CE长;
(2)求图2中的PH长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A在坐标原点,∠CAB=45°,AC=2![]() ,∠ACB=60°,点B在x轴正半轴,点C在第一象限,动点D在边AB上运动,以CD为直径作⊙O与AC,AB分别交于E,F,连接EF.
,∠ACB=60°,点B在x轴正半轴,点C在第一象限,动点D在边AB上运动,以CD为直径作⊙O与AC,AB分别交于E,F,连接EF.
(1)当△CEF成为等边三角形时,AE:EC= ;
(2)当EF=![]() 时,点D的坐标为 .
时,点D的坐标为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com