
| A. | -1 | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
分析 求出数列的前4项,继而得出数列的循环周期,然后根据所得的规律进行求解即可.
解答 解:∵a1=$\frac{1}{2}$,an=$\frac{1}{1{-a}_{n-1}}$,
∴a2=$\frac{1}{1-{a}_{1}}$=$\frac{1}{1-\frac{1}{2}}$=2,
a3=$\frac{1}{1-{a}_{2}}$=$\frac{1}{1-2}$=-1,
a4=$\frac{1}{1-{a}_{3}}$=$\frac{1}{1-(-1)}$=$\frac{1}{2}$,
…
∴这列数每3个数为一循环周期,
∵2017÷3=672…1,
∴a2017=a1=$\frac{1}{2}$,
故选B.
点评 此题主要考查了数字变化规律问题,认真观察、仔细思考,善用联想是解决这类问题的方法,解题时注意运用an=$\frac{1}{1{-a}_{n-1}}$进行计算.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
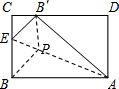 将矩形纸片ABCD折叠,使点B落在边CD上的B'处,折痕为AE,已知AB=5,AD=4.
将矩形纸片ABCD折叠,使点B落在边CD上的B'处,折痕为AE,已知AB=5,AD=4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | 0 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com