
分析 (1)先把各二次根式化为最简二次根式,然后合并即可;
(2)根据二次根式的乘除法则运算.
解答 解:(1)原式=2$\sqrt{6}$-3$\sqrt{2}$-$\frac{1}{6}\sqrt{6}$+$\sqrt{2}$
=$\frac{11}{6}\sqrt{6}$-2$\sqrt{2}$;
(2)原式=12$\sqrt{3}$÷$\frac{\sqrt{30}}{2}$•$\frac{\sqrt{30}}{3}$
=12$\sqrt{3}$×$\frac{2}{\sqrt{30}}$•$\frac{\sqrt{30}}{3}$
=8$\sqrt{3}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线y=2x-4分别交坐标轴于A、B两点,交双曲线y=$\frac{k}{x}$(x>0)于C点,且sin∠COB=$\frac{\sqrt{2}}{2}$.
如图,直线y=2x-4分别交坐标轴于A、B两点,交双曲线y=$\frac{k}{x}$(x>0)于C点,且sin∠COB=$\frac{\sqrt{2}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,以AC、BC分别向外作等边△ACF和等边△BCE,点P、M、N分别为AB、CF、CE的中点.
如图,在△ABC中,以AC、BC分别向外作等边△ACF和等边△BCE,点P、M、N分别为AB、CF、CE的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
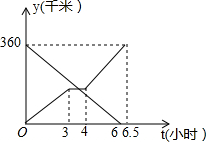 一辆货车从甲地向乙地行驶,一辆小轿车与该货车同时出发,从乙地向甲地行驶,货车匀速行驶至乙地,小轿车中途停车休整后提速行驶至甲地,货车与乙地的距离y1(千米)、小轿车与乙地的距离y2(千米)与行驶时间((小时)之间的函数关系的图象如图所示,已知当小轿车行驶2小时时,小轿车与货车相距140千米.
一辆货车从甲地向乙地行驶,一辆小轿车与该货车同时出发,从乙地向甲地行驶,货车匀速行驶至乙地,小轿车中途停车休整后提速行驶至甲地,货车与乙地的距离y1(千米)、小轿车与乙地的距离y2(千米)与行驶时间((小时)之间的函数关系的图象如图所示,已知当小轿车行驶2小时时,小轿车与货车相距140千米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在正方形ABCD中,E、F分别是AD、BC的中点,连结BE、DF,点P在DF上,且BP=BC,连接EP并延长交BC的延长线于点Q.
如图,在正方形ABCD中,E、F分别是AD、BC的中点,连结BE、DF,点P在DF上,且BP=BC,连接EP并延长交BC的延长线于点Q.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 指定日普通票 | 200元 |
| 平日优惠票 | 100元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com