
【题目】如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E,F,则线段B′F的长为( )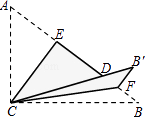
A.![]()
B.![]()
C.![]()
D.![]()
【答案】B
【解析】解:根据折叠的性质可知CD=AC=3,B′C=BC=4,∠ACE=∠DCE,∠BCF=∠B′CF,CE⊥AB,
∴B′D=4﹣3=1,∠DCE+∠B′CF=∠ACE+∠BCF,
∵∠ACB=90°,
∴∠ECF=45°,
∴△ECF是等腰直角三角形,
∴EF=CE,∠EFC=45°,
∴∠BFC=∠B′FC=135°,
∴∠B′FD=90°,
∵S△ABC= ![]() ACBC=
ACBC= ![]() ABCE,
ABCE,
∴ACBC=ABCE,
∵根据勾股定理求得AB=5,
∴CE= ![]() ,
,
∴EF= ![]() ,ED=AE=
,ED=AE= ![]() =
= ![]() ,
,
∴DF=EF﹣ED= ![]() ,
,
∴B′F= ![]() =
= ![]() .
.
所以答案是:B.
【考点精析】掌握翻折变换(折叠问题)是解答本题的根本,需要知道折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,BE和CE分别为△ABC的内角平分线和外角平分线,BE⊥AC于点H,CF平分∠ACB交BE于点F连接AE.则下列结论:①∠ECF=90°;②AE=CE;③![]() ;④∠BAC=2∠BEC;⑤∠AEH=∠BCF,正确的个数为( )
;④∠BAC=2∠BEC;⑤∠AEH=∠BCF,正确的个数为( )

A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠BAC=45°,BC=2,D是线段BC上的一个动点,点D是关于直线AB、AC的对称点分别为M、N,则线段MN长的最小值是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣x+1与x轴,y轴分别交于B,A两点,动点P在线段AB上移动,以P为顶点作∠OPQ=45°交x轴于点Q.

(1)求点A和点B的坐标;
(2)比较∠AOP与∠BPQ的大小,说明理由.
(3)是否存在点P,使得△OPQ是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:点![]() 不在同一条直线,
不在同一条直线,![]() .
.
(1)求证:![]() .
.
(2)如图②,![]() 分别为
分别为![]() 的平分线所在直线,试探究
的平分线所在直线,试探究![]() 与
与![]() 的数量关系;
的数量关系;
(3)如图③,在(2)的前提下,且有![]() ,直线
,直线![]() 交于点
交于点![]() ,
,![]() ,请直接写出
,请直接写出![]() ______________.
______________.
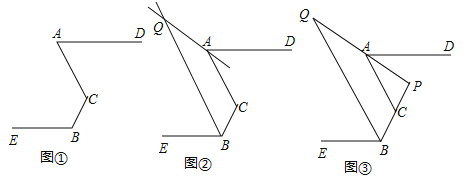
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠B=90°,AB∥CD,M为BC边上的一点,且AM平分∠BAD,DM平分∠ADC.
求证:(1)AM⊥DM;
(2)M为BC的中点.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C,D在AB同侧,∠CAB=∠DBA,下列条件中不能判定△ABD≌△BAC的是( )

A. ∠D=∠C B. BD=AC C. ∠CAD=∠DBC D. AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八(1)班同学为了解2018年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,请解答以下问题:


(1)本次调查采用的调查方式是________(填“普查”或“抽样调查”),样本容量是________;
(2)补全频数分布直方图:
(3)若将月均用水量的频数绘成扇形统计图,则月均用水量“![]() ”的圆心角度数是________;
”的圆心角度数是________;
(4)若该小区有5000户家庭,求该小区月均用水量超过![]() 的家庭大约有多少户?
的家庭大约有多少户?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com