
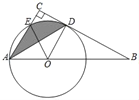
【题目】如图,点O为Rt△ABC斜边AB上的一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD.
(1)求证:AD平分∠BAC;
(2)若∠BAC=60°,OA=2,求阴影部分的面积(结果保留π).
【答案】(1)证明见解析;(2)![]()
【解析】
(1)由Rt△ABC中,∠C=90°,⊙O切BC于D,易证得AC∥OD,继而证得AD平分∠CAB.
(2)如图,连接ED,根据(1)中AC∥OD和菱形的判定与性质得到四边形AEDO是菱形,则△AEM≌△DMO,则图中阴影部分的面积=扇形EOD的面积.
(1)证明:∵⊙O切BC于D,
∴OD⊥BC,
∵AC⊥BC,
∴AC∥OD,
∴∠CAD=∠ADO,
∵OA=OD,
∴∠OAD=∠ADO,
∴∠OAD=∠CAD,
即AD平分∠CAB;
(2)设EO与AD交于点M,连接ED.
∵∠BAC=60°,OA=OE,
∴△AEO是等边三角形,
∴AE=OA,∠AOE=60°,
∴AE=AO=OD,
又由(1)知,AC∥OD即AE∥OD,
∴四边形AEDO是菱形,则△AEM≌△DMO,∠EOD=60°,
∴S△AEM=S△DMO,
∴S阴影=S扇形EOD=![]() =
=![]() π.
π.


 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案科目:初中数学 来源: 题型:
【题目】环保局对某企业排污情况进行检测,结果显示,所排污水中硫化物的浓度超标,即硫化物的浓度超过最高允许的![]() ,环保局要求该企业立即整改,在15天以内(含15天)排污达标,整改过程中,所排污水中硫化物的浓度
,环保局要求该企业立即整改,在15天以内(含15天)排污达标,整改过程中,所排污水中硫化物的浓度![]() 与时间
与时间![]() (天)的变化规律如图所示,其中线段
(天)的变化规律如图所示,其中线段![]() 表示前3天的变化规律,从第3天起,所排污水中硫化物的浓度
表示前3天的变化规律,从第3天起,所排污水中硫化物的浓度![]() 与时间
与时间![]() 成反比例关系
成反比例关系
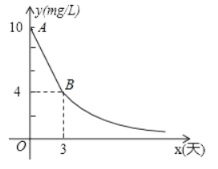
(1)求整改过程中硫化物的浓度![]() 与时间
与时间![]() 的函数表达式(要求标注自变量
的函数表达式(要求标注自变量![]() 的取值范围)
的取值范围)
(2)该企业所排污水中硫化物的浓度,能否在15天以内(含15天)排污达标?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣4x+3.
(1)求该二次函数与x轴的交点坐标和顶点;
(2)在所给坐标系中画出该二次函数的大致图象,并写出当y<0时,x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市为庆祝开业举办大酬宾抽奖活动,凡在开业当天进店购物的顾客,都能获得一次抽奖的机会,抽奖规则如下:在一个不透明的盒子里装有分别标有数字1、2、3的3个小球,它们的形状、大小、质地完全相同,顾客先从盒子里随机取出一个小球,记下小球上标有的数字,然后把小球放回盒子并搅拌均匀,再从盒子中随机取出一个小球,记下小球上标有的数字,并计算两次记下的数字之和,若两次所得的数字之和为6,则可获得50元代金券一张;若所得的数字之和为5,则可获得30元代金券一张;若所得的数字之和为4,则可获得15元代金券一张;其它情况都不中奖.
(1)请用列表或树状图的方法(选其中一种即可),把抽奖一次可能出现的结果表示出来.
(2)假如你参加了该超市开业当天的一次抽奖活动,求能中奖的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交![]() 于点E,以点O为圆心,OC的长为半径作
于点E,以点O为圆心,OC的长为半径作![]() 交OB于点D.若OA=4,则图中阴影部分的面积为( )
交OB于点D.若OA=4,则图中阴影部分的面积为( )
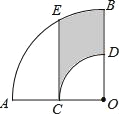
A. ![]() +
+![]() B.
B. ![]() +2
+2![]() C.
C. ![]() +
+![]() D. 2
D. 2![]() +
+![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
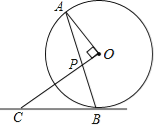
【题目】如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的直线交OP的延长线于点C,且CP=CB.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为![]() ,OP=1,求BC的长.
,OP=1,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象的顶点在第一象限,且过点(0,1)和(﹣1,0).下列结论:①ab<0,②b2>4a,③0<a+b+c<2,④0<b<1,⑤当x>﹣1时,y>0,其中正确结论的个数是
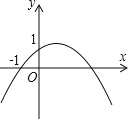
A.5个 B.4个 C.3个 D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一电线杆AB的影子分别落在了地上和墙上.同一时刻,小明竖起1米高的直杆MN,量得其影长MF为0.5米,量得电线杆AB落在地上的影子BD长3米,落在墙上的影子CD的高为2米.你能利用小明测量的数据算出电线杆AB的高吗?
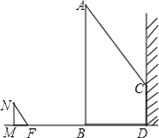
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】被誉为“中原第一高楼”的郑州会展宾馆(俗称“玉米楼”)坐落在风景如画的如意湖畔,是来郑州观光的游客留影的最佳景点.学完了三角函数知识后,刘明和王华决定用自己学到的知识测量“玉米楼”的高度.如图,刘明在点C处测得楼顶B的仰角为45°,王华在高台上的D处测得楼顶的仰角为40°.若高台DE的高为5米,点D到点C的水平距离EC为47.4米,A,C,E三点共线,求“玉米楼”AB的高度.(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,结果保留整数)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com