
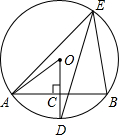
 如图,AB是⊙O的一条弦,点D是弧AB的中点,OD交AB于点C,点E在⊙O上. 若∠OAC=40°,求∠DEB的度数.
如图,AB是⊙O的一条弦,点D是弧AB的中点,OD交AB于点C,点E在⊙O上. 若∠OAC=40°,求∠DEB的度数. 分析 先根据圆心角、弧、弦的关系得出$\widehat{AD}$=$\widehat{BD}$,AB⊥OD,故可得出∠DEB=$\frac{1}{2}$∠AOD,由直角三角形的性质求出∠AOD的度数即可.
解答 解:∵点D是弧AB的中点,
∴$\widehat{AD}$=$\widehat{BD}$,AB⊥OD,
∴∠DEB=$\frac{1}{2}$∠AOD.
∵∠OAC=40°,
∴∠AOD=90°-40°=50°,
∴∠DEB=$\frac{1}{2}$∠AOD=25°.
点评 本题考查的是圆周角定理,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解答此题的关键.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 列方程解应用题:
列方程解应用题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 439名学生是总体 | B. | 每名学生是个体 | ||
| C. | 这个样本容量是45 | D. | 45名学生是所抽取的一个样本 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,⊙O的直径AB垂直于弦CD,垂足为E,AE=1,CD=2$\sqrt{3}$.
如图,⊙O的直径AB垂直于弦CD,垂足为E,AE=1,CD=2$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com