
分析 (1)根据长方形的性质可得点B的横坐标与点C的横坐标相同,纵坐标与点A的纵坐标相同,然后写出即可;再求出t=15时点P的位置,然后写出点P的坐标;
(2)分点P在OC和AB上两种情况讨论求解;
(3)分三种情况讨论:点P在点Q的前面;点P在点Q的后面;点Q停止,点P运动,分别根据路程的关系列出方程求解即可.
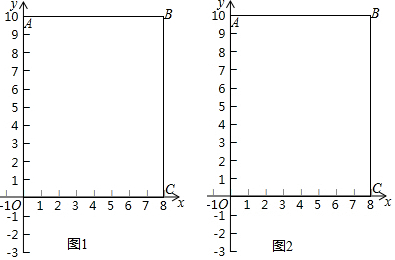
解答 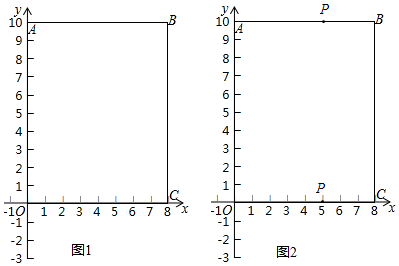 解:(1)如图1,∵长方形OABC中,AB∥CO,BC∥AO,A(0,10),C(8,0),
解:(1)如图1,∵长方形OABC中,AB∥CO,BC∥AO,A(0,10),C(8,0),
∴点B的横坐标为8,纵坐标为10,
∴点B(8,10),
当t=15时,15-10=5<8,
∴点P在AB上,且到点A的距离为5,
∴此时,点P坐标为(5,10);
(2)如图2,当点P在AB上时,PB=3,
∴t=(10+8-3)÷1=15秒;
当点P在OC上时,PC=3,
∴t=(10+8+10+3)÷1=31秒,
∴点P运动的时间为15秒或31秒,
故答案为:15或31;
(3)∵D为BC的中点,
∴BD=5=DC,即D(8,5),
若点P在点Q前面,设点Q运动x秒时,点P、Q在运动路线上相距的路程为4个单位长度,
故x+10=4+2x,
∴x=6,
此时,点P在AB上,AP=6×1=6,PB=8-6=2,如图3,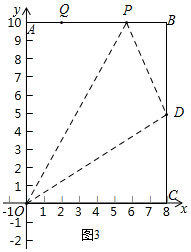
∴△ODP的面积=梯形AODB的面积-△AOP的面积-△BDP的面积
=$\frac{(5+10)×8}{2}$-$\frac{1}{2}$×6×10-$\frac{1}{2}$×2×5
=60-30-5
=25;
若点P在点Q后面,设点Q运动x秒时,点P、Q在运动路线上相距的路程为4个单位长度,
则2x=10+x+4,
∴x=14,
此时,点P在BC上,BP=14-8=6,DP=BP-BD=6-5=1,如图4,
∴△ODP的面积=$\frac{1}{2}$×DP×OC=$\frac{1}{2}$×1×8=4;
若点Q到达点O停止运动,而点P运动,则当点P、Q在运动路线上相距的路程为4个单位长度时,点P在OC上,OP=4,如图5,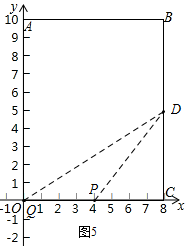
∴△ODP的面积=$\frac{1}{2}$×OP×CD=$\frac{1}{2}$×4×5=10.
综上所述,当P、Q在运动路线上相距的路程为4个单位长度时,△ODP的面积为25或4或10.
点评 本题属于四边形综合题,主要考查了矩形的性质,三角形的面积计算等知识点,解题时注意分类讨论思想的运用,在分类时要注意不能遗漏,也不能重复.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:选择题
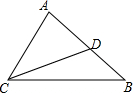 如图,下列条件:①∠B=∠ACD;②∠ADC=∠ACB;③AC2=AD•AB;④$\frac{AC}{CD}=\frac{AB}{BC}$,其中能够判定△ABC∽△ACD的个数为( )
如图,下列条件:①∠B=∠ACD;②∠ADC=∠ACB;③AC2=AD•AB;④$\frac{AC}{CD}=\frac{AB}{BC}$,其中能够判定△ABC∽△ACD的个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
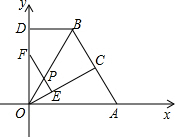 如图,OA=OB=10,AB=12,点A在x轴正半轴上,过点O作OC⊥AB于点C,作BD垂直y轴于D,若动点E从原点O出发,沿线段OC向终点C运动,动点F从点D出发,沿线段DO向终点O运动,两点同时出发,速度均为每秒1个单位长度,设运动的时间为t秒.
如图,OA=OB=10,AB=12,点A在x轴正半轴上,过点O作OC⊥AB于点C,作BD垂直y轴于D,若动点E从原点O出发,沿线段OC向终点C运动,动点F从点D出发,沿线段DO向终点O运动,两点同时出发,速度均为每秒1个单位长度,设运动的时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
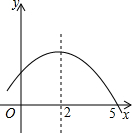 如图是二次函数y=ax2+bx+c的部分图象,由图象可知不等式ax2+bx+c>0的解集是( )
如图是二次函数y=ax2+bx+c的部分图象,由图象可知不等式ax2+bx+c>0的解集是( )| A. | -1<x<5 | B. | x>5 | C. | x<-1 | D. | x<-1或x>5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com