Question

1．如图，两张48×40的长方形纸片有一个顶点重合，重叠放置的尺寸如图所标示，则图中阴影部分的面积=984．

Answer 1

分析 在两个直角三角形中根据勾股定理求出EF=30，再面积之差求出阴影部分面积即可．

解答 解：如图，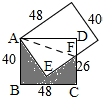

连接AF，根据题意得，CD=AB=AE=40，BC=AD=48，CF=26，
∴DF=CD-CF=40-24=14，
∵四边形ABCD是长方形，
∴∠ADF=90°，
在Rt△ADF中，AD=48，DF=14，
∴AF²=AD²+DF²
在Rt△AEF中，AE=40，
∴EF²=AF²-AE²=AD²+DF²-AE²=AD²+DF²-AE²=48²+14²-40²=30²，
∴EF=30，
∴S_阴影=S_梯形ABCF-S_△AEF=$\frac{1}{2}$（CF+AB）×BC-$\frac{1}{2}$AE×EF=$\frac{1}{2}$（26+40）×48-$\frac{1}{2}$×40×30=984．
故答案为：984

点评 此题是面积与等积变换，主要考查了长方形的性质，勾股定理，三角形的面积，梯形的面积，求出EF是解本题的关键．