
【题目】如图,在平行四边形ABCD中,分别以AB、AD为边向外作等边△ABE、△ADF,延长CB交AE于点G,点G在点A、E之间,连接CE、CF,EF,则以下四个结论一定正确的是:①△CDF≌△EBC;②∠CDF=∠EAF;③△ECF是等边△;④CG⊥AE( )
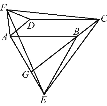
A. 只有①② B. 只有①②③ C. 只有③④ D. ①②③④
【答案】B
【解析】根据题意,结合图形,对选项一一求证,判定正确选项
解:在□ABCD中,∠ADC=∠ABC,AD=BC,CD=AB,
∵△ABE、△ADF都是等边三角形,
∴AD=DF,AB=EB,∠ADF=∠ABE=60°,
∴DF=BC,CD=BC,
∴∠CDF=360°-∠ADC-60°=300°-∠ADC,
∠EBC=360°-∠ABC-60°=300°-∠ABC,
∴∠CDF=∠EBC,
在△CDF和△EBC中,
DF=BC,∠CDF=∠EBC,CD=EB,
∴△CDF≌△EBC(SAS),故①正确;
在ABCD中,∠DAB=180°-∠ADC,
∴∠EAF=∠DAB+∠DAF+∠BAE=180°-∠ADC+60°+60°=300°-∠ADC,
∴∠CDF=∠EAF,故②正确;
同理可证△CDF≌△EAF,
∴EF=CF,
∵△CDF≌△EBC,
∴CE=CF,
∴EC=CF=EF,
∴△ECF是等边三角形,故③正确;
当CG⊥AE时,∵△ABE是等边三角形,
∴∠ABG=30°,
∴∠ABC=180°-30°=150°,
∵∠ABC=150°无法求出,故④错误;
综上所述,正确的结论有①②③.
故选B.
“点睛”本题考查了全等三角形的判定、等边三角形的判定和性质、平行线的性质等知识,综合性强,考查学生综合运用数学知识的能力.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,P是等腰直角△ABC外一点,把BP绕点B顺时针旋转90°到BP′,已知∠AP′B=135°,P′A:P′C=1:3,则P′A:PB=( ) 
A.1: ![]()
B.1:2
C.![]() :2
:2
D.1: ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD为平行四边形,AE⊥BD于E,CF⊥BD于F. 
(1)求证:BE=DF;
(2)若 M、N分别为边AD、BC上的点,且DM=BN,试判断四边形MENF的形状(不必说明理由).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】深化理解:
新定义:对非负实数x “四舍五入”到个位的值记为![]() ,
,
即:当n为非负整数时,如果![]() ;
;
反之,当n为非负整数时,如果![]()
例如:<0> = <0.48> = 0,<0.64> = <1.49> = 1,<2> = 2,<3.5> = <4.12> = 4,……
试解决下列问题:
(1)填空:①![]() =________(
=________(![]() 为圆周率); ②如果
为圆周率); ②如果![]() 的取值范围为____________________.
的取值范围为____________________.
(2)若关于x的不等式组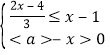 的整数解恰有3个,求a的取值范围.
的整数解恰有3个,求a的取值范围.
(3)求满足![]() 的所有非负实数x的值.
的所有非负实数x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了更好地治理小凌河水质,保护环境,市治污公司决定购买10台污水处理设备,现有A 、B两种设备,A 、B单价分别为a万元/台、 b万元/台,月处理污水分别为240吨/月、200吨/月,经调查,买一台A型设备比买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
(1)求a、b的值.
(2)经预算,市治污公司购买污水处理器的资金不超过105万元,你认为该公司有哪几种购买方案?
(3)在(2)的条件下,若每月处理的污水不低于2040吨,为了节约资金,请你为治污公司设计一种最省钱的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是正方形ABCD内的一点,连接AE、BE、CE,将△ABE绕点B顺时针旋转90°到△CBE′的位置.若AE=1,BE=2,CE=3,则∠BE′C=__度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.在直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E.那么点D的坐标为( ) 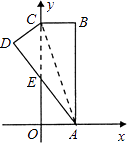
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com