练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    18．菱形ABCD中，E、F是AB和AC的中点，EF=1，则菱形ABCD的周长为8．

    分析 根据题意可得出EF是△ABC的中位线，易得BC长为EF长的2倍，那么菱形ABCD的周长=4BC．

    解答 解：如图所示：
    ∵AC是菱形ABCD的对角线，E、F分别是AB、AC的中点，
    ∴EF是△ABC的中位线，
    ∴EF=$\frac{1}{2}$BC=1，
    ∴BC=2，
    ∴菱形ABCD的周长是4×2=8．
    故答案为：8．

    点评 本题考查的是三角形中位线的性质及菱形的性质，关键是根据EF是△ABC的中位线，得出BC的长度．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

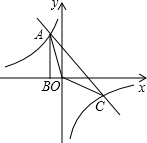    8．如图，Rt△ABO的顶点A是双曲线y=$\frac{k}{x}$与y=-x-（k+1）在第二象限的交点，AB⊥x轴于B且S△ABO=$\frac{3}{2}$．
    （1）求这两个函数的关系式；
    （2）根据图象写出使一次函数的值小于反比例函数的值的x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．计算：
    （1）（-2016）0+（-$\frac{1}{3}$）-2
    （2）|1-$\sqrt{2}$|-2cos45°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．已知：CD为△ABC的外角平分线，交△ABC的外接圆O于D．
    （1）如图1，连接OA，OD，求证：∠AOD=2∠BCD；
    （2）如图2，若CB平分∠ACD，求证：AB=BD；
    （3）在（2）的条件下，若⊙O的半径为$\frac{2\sqrt{15}}{3}$，tan∠ABC=$\frac{1}{2}$，求CD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

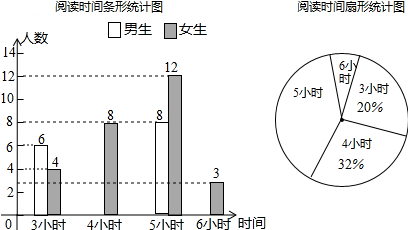
    13．为调查聊城市某村开展“要致富，多读书”活动的效果，小红利用周末随机抽查了该村部分村民在一周内的阅读时间，并将结果绘制成如图两幅不完整的统计图，则本次调查的阅读时间的中位数和众数分别为（　　）
    A．4小时，5小时B．5小时，4小时C．4小时，4小时D．5小时，5小时

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．一个不透明的矩形容器里装有10个小球（除颜色外完全相同），其中4个白球，6个红球，现从容器中摸出两个球，则摸到相同颜色的球的概率是$\frac{7}{15}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．下列四个实际问题中的两个变量之间关系中，属于正比例函数关系的是（　　）
    A．有一个边长为x的正方体，则它的表面积S与边长x之间的函数关系
    B．某梯形的下底5cm，高3cm，上底xcm（0＜x＜5），则梯形的面积S与上底x之间的函数关系
    C．一个质量为100kg的物体，静止放在桌面上，则该物体对桌面的压强P与受力面面积S之间的函数关系
    D．一个小球由静止开始沿一个斜坡向下滚动，其速度每秒增加2m/s，则小球速度v与时间t之间的函数关系

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．已知函数f（x）=$\frac{1}{{2+\sqrt{x}}}$，那么f（3）=2-$\sqrt{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．计算：2tan30°-|1-$\sqrt{3}$|+（2016-$\sqrt{2}$）0+$\sqrt{\frac{1}{3}}$-（$\frac{1}{2}$）-2．

    查看答案和解析>>

    同步练习册答案